Доброго времени суток!
Не могу разобраться с интегралом

Пытаюсь контурным интегрированием
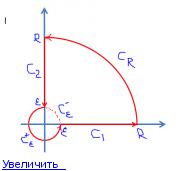
Интеграл по всему контуру

где

функция Бесселя первого рода.
Это исходя из

Вроде не сложно показывается, что интеграл (есть сомнения)

при

равен нулю:

Однако, я не смог "связать" интегралы по

и

между собой (хотя в начале показалось, что мнимая часть по

соответствует интегралу по

), тем более вычислить интеграл по

.
Выбор

вместо

ничем не помогает. Как я понимаю, что проблемы связаны с тем, что точка

существенная особая для подинтегральной функции. Ну и плюс она на одном из концов интегрирования.
Заранее благодарен за любые разъяснения.



