Добрый день, уважаемые форумчане!
Заранее, на всякий случай, оговорюсь, что я не альтернативщик и не собираюсь опровергать СТО
 Предыстория
ПредысторияВсем наверняка знаком такой вывод замедления времени.
На станции на высоте

фонарь, который светит строго вниз (рис. а). Мимо станции проезжает поезд со скоростью

. В системе отсчета поезда траектория светового луча будет иметь вид, представленный на рис. б.
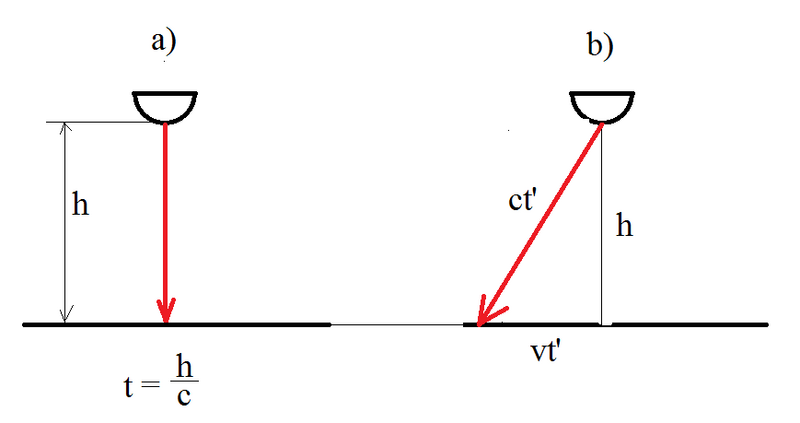
Штрихованные величины относятся к ИСО поезда, нештрихованные - к станции
Тогда, работая в ИСО поезда, по теореме Пифагора имеем:

Выражая отсюда

, получаем:

Затем, привлекая постулат о постоянстве скорости света, заключаем, что

Тогда окончательно
 Мой вопрос
Мой вопросЧто если изначально мы предполагаем, что в ИСО станции луч был направлен под углом, скажем,

(рис. а)?
Тогда, насколько я понимаю, в ИСО поезда траектория будет иметь вид как на рис. б.
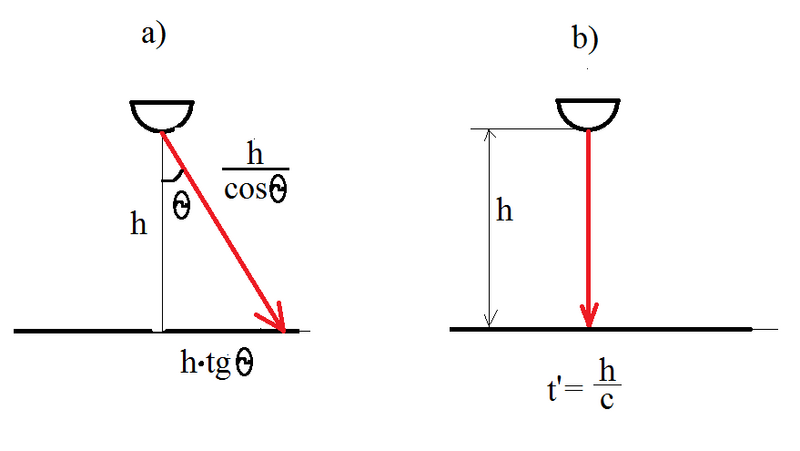
При этом, исходя из рисунков, времена будут соответственно равняться

и

И я не совсем понимаю, как в этой ситуации можно получить замедление времени Лоренца?
Заранее благодарен за любую помощь!



