пусть есть функции

и
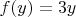
Это не две функции, это одна и та же функция

.
Это функция, умножающая свой аргумент на

.
Если мы подставляем в эту функцию

, она умножает его на

и получается
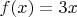
.
Если мы подставляем в эту функцию

, она умножает его на

и получается
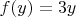
.
Если мы подставляем в эту функцию число

, она умножает его на

и получается

.
Чтобы не говорить словами:

- функция, умножающая свой аргумент на

, этот "свой аргумент" обозначают какой-нибудь буквой, например

, и пишут: функция

определена формулой
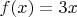
.
Но точно так же можно сказать: функция

определена формулой
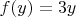
.
Между этими двумя предложениями нет никакой разницы; неважно, какой буквой обозначать аргумент функции.
пусть есть функции
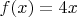
и

Так нельзя говорить. Функция - это не

и не

; функция - это

.
Если Вы определяете функцию

формулой

, то вместо

сюда можно подставлять всё что угодно, в том числе можно вместо

подставить

, и тогда автоматически будет

. А не
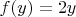
, как Вы написали.
Заметьте! Для какой-нибудь функции

и каких-нибудь чисел

вполне может оказаться так, что

, но
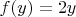
. Например если взять функцию

, и взять числа

. Тогда будем иметь

.
То есть в принципе, утверждения

и
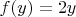
друг другу не противоречат.
Дьявол кроется в деталях: не в формулах, а в словах, которые сказаны вокруг этих формул.
Если сказано: "для каких-то значений

справедливо

и
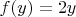
" - то тут нет никакого противоречия, см. пример в предыдущем абзаце.
А если сказано "функция

определена формулой

" (подразумевается, что формула справедлива для всех

, а не только для какого-то конкретного), то эта функция никак не может быть вместе с этим определена формулой
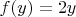
. Здесь уже будет противоречие.
Когда в учебниках говорят "рассмотрим функцию

" (или вместо

любая другая формула), имеют в виду, что эта формула должна быть справедлива при любых

, а не только при каком-то конкретном. И это надо хорошо понимать и иметь в виду.