Из 1го тома Фихтенгольца:

Я пока не очень уверен в этой теме. Поясню на примере.
Пусть есть функция

.
Тогда:
1) для вычисления

делаем подстановку в

, заменяя

на

:

2) для вычисления

делаем подстановку в

, заменяя

на

:

Это вроде ясно.
Далее: пусть есть функции

и
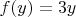
, тогда:
1) для вычисления

делаем подстановку в

, заменяя

на

:

или
2) для вычисления

делаем подстановку в

, заменяя

на

:

Вопросы:
1) пусть есть функции
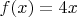
и

, как вычислить, чему равно

?
Спрашиваю, потому что при попытке подстановок как в примерах выше не получается однозначного результата:
- при замене

на

в

получаем:

;
- при замене

на

в

получаем:

;
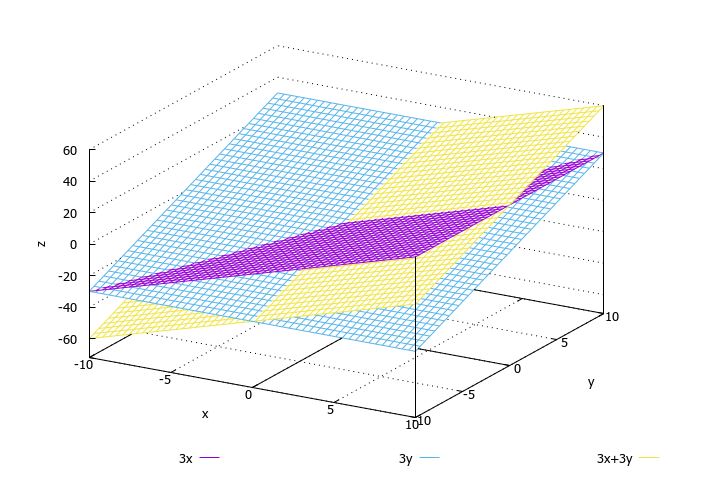
2) как связаны между собой графики функций

,

и

? Если предположить, что речь о именно трёхмерном пространстве, тогда получаем такие уравнения:

,

,

и такие графики: