Концепция отрицательных чисел не зря вызывала трудности у математиков прошлого :)
Мне в школе помогали именно представления
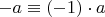
и

с учетом

Кстати, википедия об этой "несуразности" тоже знает:
Цитата:
Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия.
Мы просто привыкли. Когда в школе я сделал вышеприведенное открытие с тождествами (не помню к каком классе, вероятно в том, где требовалось раскрывать скобки или наоборот), мир заиграл для меня новыми красками. Возможно, теперь и у ТС-а заиграет.



