It should not be a hard problem, but it is possible to make a mistake while solving it. That is the reason I think it is suitable for lower rounds of a math olympiad. I found the problem in an old magazine from Sweden (1942) as a statement (there was no solution). I made some attempts to solve it.
From the first equation we have
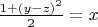
*)
From the second equation we have
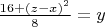
**)
Then from *) - **) we have:
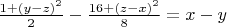
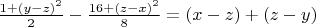
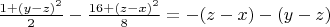
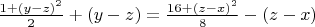
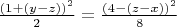
***)
Or we have two cases:

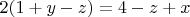

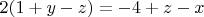
In case

there are two options:
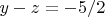
or
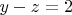
.
When
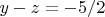
I found the following possible solutions
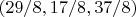
and
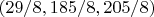
but when tried to put these values in the system's equations it turned out that the second system equation is not an identity, so only
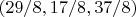
is a solution, when
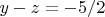
.
When
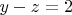
I found the following possible solutions
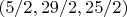
and
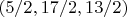
, but again the second equation is not an identity for
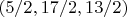
, so only
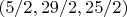
is a solution when
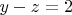
.
In case
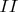
I found
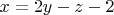
. When I tried to plug x in the system's equations I had an identity. It made me to think that the system have in this case an infinite number of solutions given by the condition:
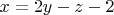
. To verify it is correct I tried to put some solutions of
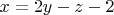
in the system's equations, but it they weren't an identities.
So I concluded - only the triples
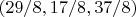
and
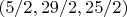
are the solutions of the system.
But ... I put the system in Wolfram Alpha and it gave a very different result:
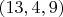
,
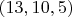
,
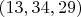
and when
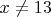
there are infinitely many solutions given by:
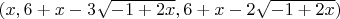
and
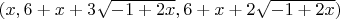
.
Probably I made a mistake or it needs more efforts in solving. Still working on it.



