Задача состоит в том что на рисунке прямоугольник делится на три равные части по следующей инструкции: проводим диагонали прямоугольника

и

, с точки пересечения диагоналей

, проводим отрезок к точке

лежащей на

, параллельный стороне

, с вершины

проводим еще один отрезок

, который пересекает диагональ в точке

, по аналогии находим точку

такую что

. Почему проекция точки

на отрезок

, отсекает ровно одну треть этого отрезка?
Могу легко доказать почему линия проведенная через центр прямоугольника

, параллельно меньшей стороне, делит большую сторону пополам с помощью признаков тождественности треугольников

и

, ниже на рисунке. Но вот с делением на три равных части, я завис как это часто случается со мной в математике...
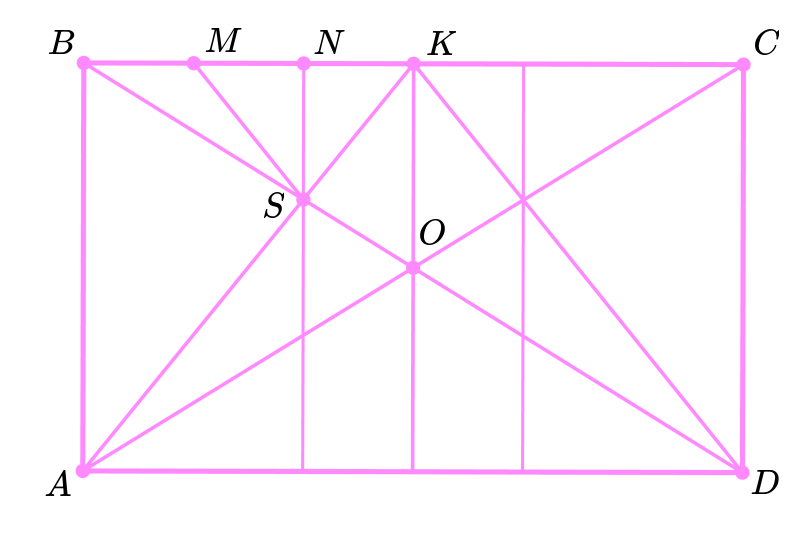
Не пойму как доказать тождественность треугольников

и

, с которой должно следовать деление на три части. Нарисовать этот прямоугольник на, опять же, плоских прямоугольных координатах, вершиной

в центре координат, и представить что

, поворачиваясь против часовой стрелки, переходит

, увеличивая при этом свой наклон в два раза, ибо с предыдущего рисунка мы знаем что точка

находится ровно середине

, сосчитать при этом координату по оси абсцисс сначала для точки

, а потом для точки

и увидеть что вторая ровно на треть меньшая за первую координату? А без координат это же должно как-то доказываться.



