Добрый вечер! Помогите, пожалуйста, понять задачу, зашел в тупик.
Тoчкa

- середина сторoны

треугольника

, в котором

- прямой,

. На отрезке

отмечена точка

такая, что

. Пусть

- высота треугольника

. Докажите, что удвоенный периметр треугольника

больше периметра треугольника

.

Медиана равна половине гипотенузы, потому ясно, что треугольник
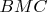
- равносторонний, также треугольник

равнобедренный с двумя углами по 30 градусов. В треуольнике

с углом в 30 градусов возьмем за

сторону

, тогда сразу получаем

. Дальнейшие действия - не очевидны. Также нашел все изображенные углы. Подскажите, пожалуйста, дальнейшие идеи?



