Вселенная Фридмана

[sergey zhukov]

Someone
Спасибо. В этой главе помимо прочего сказано:

Хорошо известно, что в классической ньютоновской теории тяготения сферически симметричное распределение вещества не создает гравитационного поля внутри сферической полости. В действительности это утверждение справедливо так же и в ОТО, если Вселенная однородна и расширяется изотропно.

Что это значит для ОТО? Разве мы можем разделить вклад в метрический тензор от вещества в пределах и за пределами сферы? Мне кажется, что в ньютоновой механике это имеет ясный смысл потому, что там решения для поля потенциала суммируются.

[Утундрий]

В ньютоновской механике имеется льющийся отовсюду яркий свет, напрочь отсутствующий в бренном не ньютоновском мире.

[Someone]

sergey zhukov в сообщении #1470561 писал(а):

Что это значит для ОТО? Разве мы можем разделить вклад в метрический тензор от вещества в пределах и за пределами сферы? Мне кажется, что в ньютоновой механике это имеет ясный смысл потому, что там решения для поля потенциала суммируются.

Ситуация в точности обратная. В ОТО происходящее следует из уравнений и начальных данных, а ньютоновская теория для величины действующей силы даёт расходящийся интеграл.

[sergey zhukov]

В книге Новикова/Зельдовича обсуждается модель Милна (вселенная Фридмана с исчезающей плотностью материи). Утверждается, что по причине фактической пустоты этой вселенной ее пространство-время плоское. Т.е. существуют координаты, в которых всюду имеем метрику плоского пространства-времени. В этих координатах ситуация выглядит, как расширяющееся облако (периферия которого удаляется со скоростью света), наблюдаемое изнутри согласно СТО.

Этот результат получается простым преобразованием координат, т.е. оба представления в точности эквивалентны.

Правильно ли я понимаю, что если бы наша вселенная действительно имела бы исчезающе малую плотность, то исходя из наблюдений мы могли бы с равными основаниями говорить как о расширении пространства отрицательной кривизны, так и о расширении облака в плоском пространстве?

Например, будет ли любая открытая вселенная Фридмана с течением времени приближаться согласно нашим наблюдениям к тому, что дает модель Милна? Или же решающее значение тут имеет начальный отрезок времени жизни любой вселенной, когда плотность ее в любом случае нельзя считать малой и этим нельзя пренебречь?

[sergey zhukov]

Часто можно услышать, что космологическое красное смещение и красное смещение из-за Доплер эффекта - это не одно и то же. Не всегда оказывается ясно, почему представление о расширении пространства - это совсем не то же самое, что представление о разлете галактик в пространстве с фиксированной метрикой (т.е. представление о том, что галактики просто разлетаются из центра взрыва в не расширяющемся пространстве).

Хотя модель обыкновенного ньютоновского взрыва (в которой самогравитирующее облако частиц разлетается из центра взрыва в пространстве с фиксированной метрикой) дает некоторые правильные результаты для космологических моделей Фридмана (зависимость масштабного фактора от времени, критическая плотность и др.), но, скажем, красное смещение эта модель простого взрыва дает неправильно. Всегда хотел нарисовать картинку, на которой эти различия становятся явными. Вот она:



Это эволюция замкнутой вселенной Фридмана, которая сначала расширяется, а затем сжимается обратно. Черным нарисована траектория произвольной частицы такой вселенной, которая излучает световые импульсы через равные промежутки времени (скажем, 1 сек). Верхняя картинка соответствует представлениям о расширении пространства (где $x$ - это расстояние вдоль $t=const$), нижняя - представлениям о разлете галактик в пространстве с фиксированной метрикой. Здесь показано поведение красного смещения фиксированного объекта во времени (а не зависимость красного смещения от расстояния для $t=const$, как о нем обычно говорят).

Лучи света на нижней картинке покидают движущуюся частицу со скоростью света и приходят к наблюдателю в момент пересечения абциссы. Видно, что наблюдатель вначале получает импульсы реже 1 сек (красное смещение), а затем - чаще 1 сек (синее смещение). Т.к. схлопывание облака осколков происходит ближе к концу в этой модели быстрее скорости света, то часть световых лучей попадает к наблюдателю уже после схлопывания (т.е. он этого уже не увидит). В этом частном случае последнее, что увидит наш наблюдатель - это момент максимального расширения облака и смену красного смещения на синее. Вторую половину событий (сжатие) он уже не увидит.

На верхней картинке лучи света от частицы визуально движутся по кривым. Правило построения их траекторий такое: скорость точки, изображающей квант света, скажем, в точке $B$ равна отрицательной константе скорости света $c=-1$ плюс скорость частицы в точке $A$, умноженной на отношение отрезков $AB$ и $BC$ (скорость частицы $U_A=\frac{dX}{dt}$). Это правило просто соответствует тому, что скорость света относительно всех частиц в облаке равна $c=-1$.

Видно, что эволюция красного смещения в этом случае выглядит не так, как в предыдущем. Качественно похоже, но количественно это не то. Особенно большая разница возникает в начале и в конце. В начале красное смещение больше, но падает оно быстрее, а в конце можно наблюдать всю историю всей вселенной, включая и синее смещение.

Вообще, можно понять почему эти модели дают разный результат. Доплер эффект в пространстве с фиксированной метрикой возникает, так сказать, в момент излучения света (зависит только от скорости источника в момент излучения), а дальше красное смещение света никак не меняется по пути к наблюдателю, оно зафиксировалось. Если же метрика пространства меняется в пространстве или во времени, то свет интегрирует красное смещение на протяжении всего своего пути от источника до наблюдателя, а не просто доносит до него информацию о скорости источника в момент излучения.

Можно сказать, что красное смещение света в этом случае зависит от скорости источника (и от расстояния до него), которая у него была на протяжении всего времени хода света от источника к приемнику, а не только от его скорости в момент излучения.

[Aritaborian]

sergey zhukov в сообщении #1548309 писал(а):

Всегда хотел нарисовать картинку, на которой эти различия становятся явными. Вот она:

Не отображается, а при попытке открыть её напрямую браузеры ругаются.

[sergey zhukov]

Интересный пример приведен в учебнике по космологии Неда Райта (да и в других он тоже упоминается).

Уравнение Фридмана $(\frac{\dot{a}}{a})^2 \propto \rho -\frac{k}{a^2}$:

Случай $\rho \to 0$ и $k=-1$ описывает практически пустую Вселенную (с бесконечно малой плотностью энергии) с отрицательной пространственной кривизной, которая расширяется с постоянной скоростью $\dot{a}=const$. Нулевая плотность энергии означает, что хотя пространственная кривизна отрицательна, пространство-время такой Вселенной плоское:



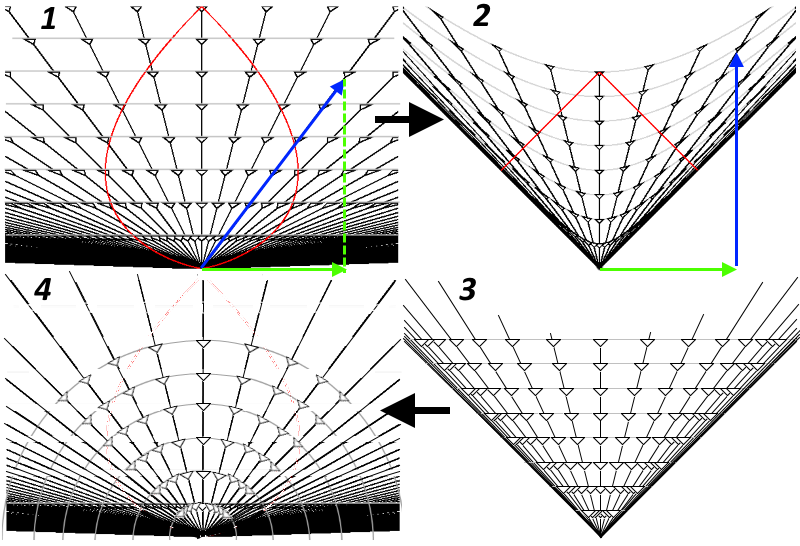
На картинке 1 нарисована такая Вселенная, в которой мировые линии частиц бесконечно малой массы являются прямыми. Плоское пространство-время означает, что для описания такой Вселенной должно быть достаточно одной только СТО.

На рисунке 2 нарисована эта же картинка, но преобразованная (радиальная координата каждой точки рисунка 1 использована, как вертикальная координата той же точки на рисунке 2). Этот рисунок напоминает рисунок, который в СТО изображает ряд наблюдателей, стартующих из общей точки так, что каждый из них имеет одну и ту же скорость $u=const$ относительно предыдущего. Это как раз и есть этот случай, только плоскости одновременности здесь выбраны не совсем привычно.

Они выбраны так, что одновременными для всех наблюдателей являются события, в которых показания их часов совпадают (общее космологическое время). Такой выбор приводит к тому, что пространство имеет не стационарную метрику (расширяется с постоянной скоростью) и имеет отрицательную кривизну, а наблюдатели в нем неподвижны и в любой момент удалены от нас на любое, в том числе и на бесконечное расстояние.

Обычно в СТО мы определяем плоскости одновременности так, как показано на рис.3. Этот выбор дает стационарное плоское пространство, которое не расширяется, а наблюдатели в нем разлетаются друг от друга с постоянными скоростями. Любой из наблюдателей (скажем $A$) видит одно и то же, а именно: все остальные удаляются от него, причем чем дальше, тем с бОльшей скоростью. На конечном расстоянии скорость удаления наблюдателей от $A$ равна скорости света. Там они сплющиваются за счет релятивистского сокращения продольной длины, расстояния между ними так же сокращаются. Плотность числа наблюдателей на метр радиальной координаты растет с приближением к границе наблюдения. За счет этого бесконечное количество наблюдателей умещается в шаре конечного размера с центром в $A$, который постоянно растет со скоростью света, и за пределами которого - пустое пространство. Часы всех окружающих $A$ наблюдателей идут медленнее за счет релятивистского замедления движущихся часов, а часы наблюдателей на границе (которые удаляются от $A$ со скоростью света) стоят. Сам $A$ наблюдает часы окружающих наблюдателей еще более замедленными за счет релятивистского эффекта Доплера.

Такую одинаковую картину видит любой из наблюдателей в этой Вселенной. Это космологическая модель Милна – модель, в которой Вселенная описывается только в рамках СТО (за счет предполагаемой бесконечно малой плотности энергии и вытекающего отсюда плоского пространства-времени). В такой модели космологическое красное смещение действительно объясняется только относительными скоростями наблюдателей, т.е. релятивистским эффектом Доплера (однако это точное совпадение существует только для Вселенной бесконечно малой плотности и связано именно с тем, что в этом случае пространство-время плоское).

Если перевести это представление на рис.3 обратно, то получим рисунок 4, где плоскости одновременности выглядят сферическими, расстояние до всех наблюдателей в любой момент времени - конечное.

Интересно, как всего лишь выбор разных координат меняет представление о кривизне и метрике пространства (плоское стационарное или отрицательно искривленное и расширяющееся), одновременности событий (общее космологическое время или замедление часов движущихся наблюдателей), движении наблюдателей (наблюдатели неподвижны в расширяющемся пространстве, или наблюдатели движутся в пространстве со стационарной метрикой), расстоянии до наблюдателей (конечное или бесконечное). Эти описания кажутся очень разными, но на самом деле это просто разные системы координат для одного и того же пространства-времени.