С решить/разобраться всё в порядке, узнал много новых слов. Ok. Частные решения не столь актуальны, поскольку выражения

и так образуют общее решение для произвольного

. Вопрос "узнаваемости"

вынесем пока за скобки.
scwec, если правильно понял, исследуя указанную Вами кривую, можем точно сказать, разрешимо ли уравнение для конкретного

и, если да, найти как минимум одно-два численных решения. Ну, Вы можете. Неважно. Возьмем

Для

, например,

или

и т.д. ..
Об общем решении и речи быть не может.
Перепишем основное уравнение так:
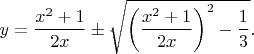
Имеем под радикалом уравнение

и одну-две рациональных точки (решения). Оно не парабола, конечно. Не проясняет это ситуацию?



