А если потребовать целочисленность

? Кажется, что все рациональные получатся и так.
Я немножко не понимаю, Вы

берете из моей формулы? Тогда всё зависит от того, сколькими способами нам удается представить

, как функцию от

. Думаю, для произвольного

вовсе не всегда возможно целое

. Но не очень понятен смысл вопроса, — перебор на такой основе будет, конечно, ущербный. Это в целых мы можем не мытьем, так катаньем, тут всё немножко по другому: понятие делимости отсутствует напрочь (как, если бы мы говорили о вычетаемости или об умножаемости)), а в понятие величины вкладывается несколько иной смысл. К примеру, приравняв

и подставив в вышеприведенные формулы, удается получить 1-параметрическое решение:
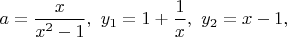
но что это значит? Заполучив фиксированное

, имеем величину и по прежнему не знаем что с ней делать кроме того, однако, что теперь можем проверить, не является ли рациональным

? Если да, то рационально и

, и вот имеем частное решение. Уже и тут без перебора не обходится, а в общем случае и подавно. Еще три примера, приведенные
nnosipov, он ведь не шутит, когда говорит:
а для  я уже не знаю, как решить уравнение в рациональных числах.
я уже не знаю, как решить уравнение в рациональных числах. Перебор, однако, несколько иного рода, и тут полезно разложение в цепную дробь, поскольку рациональное число всегда конечная дробь.
Исходное уравнение имеет рациональные решения, отличные от (0,0) только если

имеет ненулевой ранг.
А при каких

не имеет? Дайте хотя бы один пример. Остальное надо изучать, спасибо.