Нужно найти предел в пространстве D'(R) функции

.
Очевидно, что при фиксированном
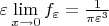
. Тогда функция

является непрерывной и ограниченной, а значит локально интегрируемой. Другими словами,

порождает регулярную обобщенную функцию.
Во всех примерах на нахождение предела обобщенной функции, что я решал все "плохое", т.е

либо уходило при замене переменной в интеграле, либо сразу можно было перейти к пределу с помощью теоремы Лебега или Римана - Лебега, здесь же.
Пусть
![$ \varphi(x) \in D(R), supp \varphi(x) \in [-R;R] $ $ \varphi(x) \in D(R), supp \varphi(x) \in [-R;R] $](https://dxdy-02.korotkov.co.uk/f/d/c/5/dc5b88e1c834060896d1855e818a786882.png)
Рассмотрим

. Как видно, переход к пределу напрямую не дает ничего хорошего, т.к

сидит в знаминателе, да ещё и с квадратом. Так же пробовал как - то добавить и отнять

и что - то пооценивать, но опять же мешает проклятый эпсилон. В общем, я совсем потерялся что делать и нуждаюсь в помощи)