public class GroupsCollection {
private static int[][][] tableSeeds = new int[100][][];
static {
// Z_2 x Z_2 x Z_2
// Order 8
tableSeeds[0] = new int[][] {
{1, 0, 4, 5, 2, 3, 7, 6},
{2, 4, 0, 6, 1, 7, 3, 5},
{3, 5, 6, 0, 7, 1, 2, 4}
};
// Tetrahredal group A_4
// Order 12
tableSeeds[1] = new int[][] {
{1, 0, 3, 2, 6, 7, 4, 5, 9, 8, 11, 10},
{2, 4, 5, 8, 9, 0, 7, 10, 11, 1, 6, 3}
};
// Z_7 # Z_3
// Order 21
tableSeeds[2] = new int[][] {
{1, 3, 4, 0, 7, 8, 9, 2, 18, 10, 6, 13, 14, 20, 15, 12, 19, 16, 5, 17, 11},
{2, 5, 6, 10, 11, 4, 12, 15, 16, 17, 8, 9, 18, 3, 1, 13, 7, 14, 20, 0, 19}
};
// Dihedral group Dih_3
// Order 6
tableSeeds[3] = new int[][] {
{1, 0, 3, 2, 5, 4},
{2, 4, 5, 1, 3, 0}
};
// Dihedral group Dih_4
// Order 8
tableSeeds[4] = new int[][] {
{1, 0, 3, 2, 6, 7, 4, 5},
{2, 4, 5, 1, 7, 6, 0, 3}
};
// Dihedral group Dih_5
// Order 10
tableSeeds[5] = new int[][] {
{1, 0, 3, 2, 6, 7, 4, 5, 9, 8},
{2, 4, 5, 1, 8, 9, 0, 3, 7, 6}
};
// Dihedral group Dih_6
// Order 12
tableSeeds[6] = new int[][] {
{1, 0, 3, 2, 6, 7, 4, 5, 11, 10, 9, 8},
{2, 4, 5, 1, 8, 9, 0, 3, 10, 11, 7, 6}
};
// Dihedral group Dih_7
// Order 14
tableSeeds[7] = new int[][] {
{1, 0, 3, 2, 6, 7, 4, 5, 10, 11, 8, 9, 13, 12},
{2, 4, 5, 1, 8, 9, 0, 3, 12, 13, 6, 7, 11, 10}
};
// Dihedral group Dih_8
// Order 16
tableSeeds[8] = new int[][] {
{1, 0, 3, 2, 6, 7, 4, 5, 10, 11, 8, 9, 15, 14, 13, 12},
{2, 4, 5, 1, 8, 9, 0, 3, 12, 13, 6, 7, 14, 15, 11, 10}
};
// Dihedral group Dih_9
// Order 18
tableSeeds[9] = new int[][] {
{1, 0, 3, 2, 6, 7, 4, 5, 10, 11, 8, 9, 14, 15, 12, 13, 17, 16},
{2, 4, 5, 1, 8, 9, 0, 3, 12, 13, 6, 7, 16, 17, 10, 11, 15, 14}
};
// Z_3 x Z_3 x Z_3
// Order 27
tableSeeds[10] = new int[][] {
{1, 4, 5, 6, 0, 10, 11, 12, 13, 14, 2, 3, 17, 18, 19, 20, 21, 7, 8, 9, 23, 24, 25, 15, 16, 26, 22},
{2, 5, 7, 8, 10, 12, 13, 0, 15, 16, 17, 18, 1, 20, 21, 3, 22, 4, 23, 24, 6, 25, 9, 11, 26, 14, 19},
{3, 6, 8, 9, 11, 13, 14, 15, 16, 0, 18, 19, 20, 21, 1, 22, 2, 23, 24, 4, 25, 5, 7, 26, 10, 12, 17}
};
// Klein group K_4
// Z_2 x Z_2
// Order 4
tableSeeds[12] = new int[][] {
{1, 0, 3, 2},
{2, 3, 0, 1}
};
// Z_3 x Z_3
// Order 9
tableSeeds[13] = new int[][] {
{1, 3, 4, 0, 6, 7, 2, 8, 5},
{2, 4, 5, 6, 7, 0, 8, 1, 3}
};
// Z_4 x Z_4
// Order 16
tableSeeds[14] = new int[][] {
{1, 3, 4, 6, 7, 8, 0, 10, 11, 12, 2, 13, 14, 5, 15, 9},
{2, 4, 5, 7, 8, 9, 10, 11, 12, 0, 13, 14, 1, 15, 3, 6}
};
// Z_5 x Z_5
// Order 25
tableSeeds[15] = new int[][] {
{1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 0, 15, 16, 17, 18, 2, 19, 20, 21, 5, 22, 23, 9, 24, 14},
{2, 4, 5, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 0, 19, 20, 21, 1, 22, 23, 3, 24, 6, 10}
};
// Z_6 x Z_6
// Order 36
tableSeeds[16] = new int[][] {
{1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 18, 19, 0, 21, 22, 23, 24, 25, 2, 26, 27, 28, 29, 5, 30, 31, 32, 9, 33, 34, 14, 35, 20},
{2, 4, 5, 7, 8, 9, 11, 12, 13, 14, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 0, 26, 27, 28, 29, 1, 30, 31, 32, 3, 33, 34, 6, 35, 10, 15}
};
// Z_7 x Z_7
// Order 49
tableSeeds[17] = new int[][] {
{1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 18, 19, 21, 22, 23, 24, 25, 26, 0, 28, 29, 30, 31, 32, 33, 2, 34, 35, 36, 37, 38, 5, 39, 40, 41, 42, 9, 43, 44, 45, 14, 46, 47, 20, 48, 27},
{2, 4, 5, 7, 8, 9, 11, 12, 13, 14, 16, 17, 18, 19, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 0, 34, 35, 36, 37, 38, 1, 39, 40, 41, 42, 3, 43, 44, 45, 6, 46, 47, 10, 48, 15, 21}
};
// Z_8 x Z_8
// Order 64
tableSeeds[18] = new int[][] {
{1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 18, 19, 21, 22, 23, 24, 25, 26, 28, 29, 30, 31, 32, 33, 34, 0, 36, 37, 38, 39, 40, 41, 42, 2, 43, 44, 45, 46, 47, 48, 5, 49, 50, 51, 52, 53, 9, 54, 55, 56, 57, 14, 58, 59, 60, 20, 61, 62, 27, 63, 35},
{2, 4, 5, 7, 8, 9, 11, 12, 13, 14, 16, 17, 18, 19, 20, 22, 23, 24, 25, 26, 27, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 0, 43, 44, 45, 46, 47, 48, 1, 49, 50, 51, 52, 53, 3, 54, 55, 56, 57, 6, 58, 59, 60, 10, 61, 62, 15, 63, 21, 28}
};
// Z_9 x Z_9
// Order 81
tableSeeds[19] = new int[][] {
{1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 18, 19, 21, 22, 23, 24, 25, 26, 28, 29, 30, 31, 32, 33, 34, 36, 37, 38, 39, 40, 41, 42, 43, 0, 45, 46, 47, 48, 49, 50, 51, 52, 2, 53, 54, 55, 56, 57, 58, 59, 5, 60, 61, 62, 63, 64, 65, 9, 66, 67, 68, 69, 70, 14, 71, 72, 73, 74, 20, 75, 76, 77, 27, 78, 79, 35, 80, 44},
{2, 4, 5, 7, 8, 9, 11, 12, 13, 14, 16, 17, 18, 19, 20, 22, 23, 24, 25, 26, 27, 29, 30, 31, 32, 33, 34, 35, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 0, 53, 54, 55, 56, 57, 58, 59, 1, 60, 61, 62, 63, 64, 65, 3, 66, 67, 68, 69, 70, 6, 71, 72, 73, 74, 10, 75, 76, 77, 15, 78, 79, 21, 80, 28, 36}
};
// Z_8 x Z_2
// Order 16
// p^8 = q^2 = I; qp = pq
tableSeeds[20] = new int[][] {
{1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 0, 15, 2},
{2, 4, 0, 6, 1, 8, 3, 10, 5, 12, 7, 14, 9, 15, 11, 13}
};
// Z_8 # Z_2
// Order 16
// p^8 = q^2 = I; qp = p^3q
tableSeeds[21] = new int[][] {
{1, 3, 4, 9, 6, 7, 5, 10, 11, 13, 8, 2, 14, 15, 0, 12},
{2, 5, 0, 8, 9, 1, 12, 13, 3, 4, 14, 15, 6, 7, 10, 11}
};
// Z_8 # Z_2
// Order 16
// p^8 = q^2 = I; qp = p^5q
tableSeeds[22] = new int[][] {
{1, 3, 4, 6, 8, 7, 10, 12, 11, 13, 9, 14, 2, 15, 5, 0},
{2, 5, 0, 8, 9, 1, 12, 13, 3, 4, 14, 15, 6, 7, 10, 11}
};
// Pauli group
// Order 16
tableSeeds[23] = new int[][] {
{1, 0, 4, 5, 2, 3, 14, 12, 10, 11, 8, 9, 7, 15, 6, 13},
{2, 6, 0, 7, 13, 11, 1, 3, 12, 10, 9, 5, 8, 4, 15, 14},
{3, 8, 9, 0, 12, 13, 11, 14, 1, 2, 15, 6, 4, 5, 7, 10}
};
// Z_4 # Z_4
// Order 16
// p^4 = q^4 = I; qp = p^3q
tableSeeds[24] = new int[][] {
{1, 3, 4, 7, 8, 2, 10, 0, 5, 6, 12, 13, 9, 15, 11, 14},
{2, 5, 6, 8, 9, 10, 11, 4, 12, 13, 14, 0, 15, 7, 1, 3}
};
// Binary tetrahedral group 2T = SL(2,3)
// Order 24
tableSeeds[30] = new int[][] {
{1, 3, 4, 11, 7, 6, 8, 17, 12, 10, 13, 16, 23, 18, 9, 19, 22, 15, 20, 2, 14, 5, 0, 21},
{2, 5, 6, 9, 3, 10, 11, 14, 7, 15, 16, 17, 20, 8, 21, 22, 12, 23, 4, 13, 1, 19, 18, 0}
};
// Symmetric group S_4
// Order 24
// r^4 = s^2 = (sr)^3 = I
tableSeeds[31] = new int[][] {
{1, 3, 4, 6, 7, 8, 0, 15, 11, 12, 13, 20, 16, 17, 18, 2, 22, 23, 21, 14, 5, 19, 9, 10},
{2, 5, 0, 9, 10, 1, 13, 14, 15, 3, 4, 19, 20, 6, 7, 8, 21, 22, 23, 11, 12, 16, 17, 18}
};
// Quaternion group Q_8 = Dic_2
// Order 8
tableSeeds[32] = new int[][] {
{1, 3, 4, 6, 7, 2, 0, 5},
{2, 5, 3, 7, 1, 6, 4, 0}
};
// Dicyclic group Dic_3
// Order 12
tableSeeds[33] = new int[][] {
{1, 3, 4, 6, 7, 2, 9, 10, 5, 11, 8, 0},
{2, 5, 6, 8, 3, 9, 10, 1, 11, 7, 0, 4}
};
// Dicyclic group Dic_4
// Order 16
tableSeeds[34] = new int[][] {
{1, 3, 4, 7, 8, 2, 10, 6, 14, 5, 13, 12, 9, 15, 11, 0},
{2, 5, 6, 9, 7, 10, 11, 12, 3, 13, 14, 0, 15, 8, 1, 4}
};
// Dicyclic group Dic_5
// Order 20
tableSeeds[35] = new int[][] {
{1, 3, 4, 7, 8, 2, 11, 10, 13, 5, 6, 15, 16, 17, 9, 18, 14, 12, 19, 0},
{2, 5, 6, 9, 10, 11, 12, 14, 7, 15, 16, 17, 0, 3, 18, 13, 19, 1, 8, 4}
};
// Dicyclic group Dic_6
// Order 24
tableSeeds[36] = new int[][] {
{1, 3, 4, 7, 8, 2, 11, 13, 14, 5, 6, 16, 17, 10, 21, 9, 20, 19, 12, 15, 23, 18, 0, 22},
{2, 5, 6, 9, 10, 11, 12, 15, 13, 16, 17, 18, 0, 19, 7, 20, 21, 22, 1, 23, 14, 3, 4, 8}
};
// Dicyclic group Dic_7
// Order 28
tableSeeds[37] = new int[][] {
{1, 3, 4, 7, 8, 2, 11, 13, 14, 5, 6, 17, 18, 16, 20, 9, 10, 22, 23, 12, 24, 15, 26, 21, 19, 0, 27, 25},
{2, 5, 6, 9, 10, 11, 12, 15, 16, 17, 18, 19, 0, 21, 13, 22, 23, 24, 25, 1, 7, 26, 20, 27, 3, 4, 14, 8}
};
// Dicyclic group Dic_8
// Order 32
tableSeeds[38] = new int[][] {
{1, 3, 4, 7, 8, 2, 11, 13, 14, 5, 6, 17, 18, 22, 20, 9, 10, 23, 24, 12, 29, 15, 16, 27, 28, 19, 0, 31, 21, 25, 26, 30},
{2, 5, 6, 9, 10, 11, 12, 15, 16, 17, 18, 19, 0, 21, 22, 23, 24, 25, 26, 1, 13, 27, 28, 29, 30, 3, 4, 20, 31, 7, 8, 14}
};
// Dicyclic group Dic_9
// Order 36
tableSeeds[39] = new int[][] {
{1, 3, 4, 7, 8, 2, 11, 13, 14, 5, 6, 17, 18, 20, 21, 9, 10, 24, 25, 12, 23, 28, 15, 16, 30, 31, 19, 0, 32, 22, 34, 29, 26, 27, 35, 33},
{2, 5, 6, 9, 10, 11, 12, 15, 16, 17, 18, 19, 0, 22, 23, 24, 25, 26, 27, 1, 29, 20, 30, 31, 32, 33, 3, 4, 13, 34, 28, 35, 7, 8, 21, 14}
};
// A_4 x Z_2
// Order 24
// a^6 = (ad)^2 = I; a^3 = d^3
tableSeeds[50] = new int[][] {
{1, 3, 4, 7, 8, 9, 10, 14, 15, 16, 5, 17, 0, 18, 12, 21, 22, 23, 11, 2, 13, 19, 6, 20},
{2, 5, 6, 11, 12, 13, 7, 15, 18, 0, 19, 4, 20, 14, 22, 9, 8, 1, 10, 23, 21, 3, 17, 16}
};
// (Z_3 x Z_3) # Z_3
// Order 27
// b^3 = c^3 = (bc)^3 = (b^2c)^3 = I
tableSeeds[53] = new int[][] {
{1, 3, 4, 0, 7, 8, 9, 2, 13, 16, 14, 18, 15, 5, 24, 21, 6, 22, 20, 23, 11, 12, 25, 26, 10, 17, 19},
{2, 5, 6, 10, 11, 12, 0, 15, 16, 17, 18, 19, 1, 20, 21, 22, 23, 24, 3, 4, 25, 26, 7, 8, 9, 13, 14}
};
// Order 48
// b^3 = c^3 = (bc)^3 = (b^2c)^4 = I
tableSeeds[54] = new int[][] {
{1, 3, 4, 0, 7, 8, 9, 2, 13, 17, 14, 19, 15, 5, 21, 26, 22, 6, 28, 23, 24, 10, 39, 11, 35, 31, 12, 37, 32, 33, 34, 45, 18, 42, 40, 20, 43, 41, 44, 16, 30, 27, 29, 46, 47, 25, 36, 38},
{2, 5, 6, 10, 11, 12, 0, 16, 17, 18, 19, 20, 1, 25, 26, 27, 28, 29, 30, 3, 4, 34, 35, 36, 31, 37, 38, 39, 7, 8, 9, 42, 41, 40, 43, 44, 45, 13, 14, 15, 47, 46, 24, 21, 22, 23, 32, 33}
};
// Order 75
// b^3 = c^3 = (bc)^3 = (b^2c)^5 = I
tableSeeds[55] = new int[][] {
{1, 3, 4, 0, 7, 8, 9, 2, 13, 17, 14, 19, 15, 5, 21, 26, 22, 6, 28, 23, 24, 10, 31, 11, 37, 32, 12, 40, 33, 34, 35, 16, 43, 18, 48, 50, 44, 20, 52, 54, 45, 46, 47, 25, 56, 27, 61, 63, 29, 64, 30, 65, 57, 58, 59, 60, 36, 38, 72, 39, 69, 41, 70, 42, 71, 67, 68, 51, 74, 55, 73, 49, 53, 62, 66},
{2, 5, 6, 10, 11, 12, 0, 16, 17, 18, 19, 20, 1, 25, 26, 27, 28, 29, 30, 3, 4, 36, 37, 38, 39, 40, 41, 42, 7, 8, 9, 47, 48, 49, 50, 51, 52, 53, 54, 55, 13, 14, 15, 59, 61, 62, 63, 64, 60, 65, 66, 56, 21, 22, 23, 24, 35, 67, 69, 70, 32, 68, 71, 72, 31, 33, 34, 73, 44, 74, 43, 45, 46, 57, 58}
};
// Order 108
// b^3 = c^3 = (bc)^3 = (b^2c)^6 = I
tableSeeds[56] = new int[][] {
{1, 3, 4, 0, 7, 8, 9, 2, 13, 17, 14, 19, 15, 5, 21, 26, 22, 6, 28, 23, 24, 10, 31, 11, 37, 32, 12, 40, 33, 34, 35, 16, 43, 18, 49, 51, 44, 20, 53, 55, 45, 46, 47, 25, 57, 27, 64, 66, 58, 29, 68, 30, 70, 59, 60, 61, 62, 36, 87, 38, 78, 39, 80, 82, 41, 83, 42, 85, 73, 74, 75, 76, 77, 50, 99, 52, 92, 94, 54, 95, 56, 96, 98, 88, 89, 90, 91, 48, 65, 105, 67, 101, 71, 102, 72, 104, 100, 103, 63, 69, 81, 86, 106, 107, 79, 84, 93, 97},
{2, 5, 6, 10, 11, 12, 0, 16, 17, 18, 19, 20, 1, 25, 26, 27, 28, 29, 30, 3, 4, 36, 37, 38, 39, 40, 41, 42, 7, 8, 9, 48, 49, 50, 51, 52, 53, 54, 55, 56, 13, 14, 15, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 21, 22, 23, 24, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 31, 32, 33, 34, 35, 90, 92, 93, 94, 95, 91, 96, 97, 98, 99, 43, 44, 45, 46, 47, 100, 101, 102, 58, 103, 104, 105, 57, 59, 60, 61, 62, 106, 107, 73, 74, 75, 76, 88, 89}
};
// Symmetric group S_5
// Order 120
// r^5 = s^2 = (sr)^4 = (sr^2sr^3)^2 = I
tableSeeds[60] = new int[][] {
{1, 3, 4, 6, 7, 8, 11, 12, 13, 14, 15, 0, 19, 20, 21, 22, 23, 24, 25, 2, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 26, 5, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 9, 10, 66, 67, 68, 69, 70, 71, 72, 73, 87, 74, 75, 76, 77, 78, 79, 80, 81, 82, 16, 17, 18, 30, 88, 89, 90, 91, 92, 93, 94, 83, 65, 95, 96, 97, 98, 99, 100, 101, 102, 103, 27, 28, 29, 107, 108, 109, 110, 111, 112, 85, 61, 104, 86, 64, 113, 114, 60, 117, 115, 41, 43, 44, 45, 118, 119, 84, 42, 116, 105, 106, 62, 63},
{2, 5, 0, 9, 10, 1, 16, 17, 18, 3, 4, 26, 27, 28, 29, 30, 6, 7, 8, 25, 41, 42, 43, 44, 45, 19, 11, 12, 13, 14, 15, 40, 49, 60, 52, 61, 62, 63, 64, 65, 31, 20, 21, 22, 23, 24, 58, 59, 71, 32, 83, 73, 34, 84, 76, 85, 86, 87, 46, 47, 33, 35, 36, 37, 38, 39, 80, 81, 82, 103, 92, 48, 104, 51, 105, 98, 54, 93, 106, 88, 66, 67, 68, 50, 53, 55, 56, 57, 79, 101, 102, 111, 70, 77, 107, 116, 113, 114, 75, 112, 117, 89, 90, 69, 72, 74, 78, 94, 109, 108, 115, 91, 99, 96, 97, 110, 95, 100, 119, 118}
};
}
public static int[][] getTableSeed(int arg) {
return tableSeeds[arg];
}
}



 , и может ещё несколько раз так сделать?
, и может ещё несколько раз так сделать? :
: с таблицей умножения:
с таблицей умножения:
 комбинации, что даёт 24 автоморфизма группы тетраэдра
комбинации, что даёт 24 автоморфизма группы тетраэдра  .
.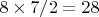 , а всего
, а всего  . Казалось бы получили те же самые 24 автоморфизма. Ан нет!
. Казалось бы получили те же самые 24 автоморфизма. Ан нет! ), а некоторых — 3-го (например,
), а некоторых — 3-го (например,  ). Поэтому эти 24 порождающих множества дальше распадаются на два класса по 12 множеств. Внутри каждого этого класса теперь пары можно не только переставлять, но и заменять друг на друга. Получается как раз 24 автоморфизма.
). Поэтому эти 24 порождающих множества дальше распадаются на два класса по 12 множеств. Внутри каждого этого класса теперь пары можно не только переставлять, но и заменять друг на друга. Получается как раз 24 автоморфизма.

 . Распознавание групп по таблице умножения — та ещё проблема.
. Распознавание групп по таблице умножения — та ещё проблема.







 можно выразить в виде произведения автоморфизмов:
можно выразить в виде произведения автоморфизмов:  , если числа n и m являются взаимно простыми. Сейчас пытаюсь понять, откуда все эти закономерности берутся.
, если числа n и m являются взаимно простыми. Сейчас пытаюсь понять, откуда все эти закономерности берутся. , порядок которой 168 не смотря на то, что порядок исходной группы всего 8!
, порядок которой 168 не смотря на то, что порядок исходной группы всего 8! однозначно задается образом единицы. А в какие элементы может перейти
однозначно задается образом единицы. А в какие элементы может перейти  , чтобы получился автоморфизм?
, чтобы получился автоморфизм? собрать автоморфизм
собрать автоморфизм  , а потом его разобрать обратно на пару.
, а потом его разобрать обратно на пару. имеет ранг 2 и может быть представлено в виде произведения
имеет ранг 2 и может быть представлено в виде произведения  , где
, где  , но
, но  . Если потребовать, чтобы число
. Если потребовать, чтобы число  , но весьма хитро выражается. Я замечал некоторые закономерности, но пока не нашёл общей формулы.
, но весьма хитро выражается. Я замечал некоторые закономерности, но пока не нашёл общей формулы. имеет ранг 1, а когда 2, заметили? Это будет подсказкой, как посчитать
имеет ранг 1, а когда 2, заметили? Это будет подсказкой, как посчитать  (в частности,
(в частности,  если ранг 1).
если ранг 1). имеет ранг 1, а когда 2, заметили?
имеет ранг 1, а когда 2, заметили? каждый следующий порядок должен делить предыдущий.
каждый следующий порядок должен делить предыдущий.