Прежде всего заметим, что поведение решения имеет смысл обсуждать только после того, как мы установим их существование.
Задача плохо поставлена без условия
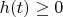
. Если

и
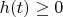
при

, то задача хорошо поставлена.
Ой, да, извиняюсь, всё именно так: решение интересует на

,
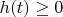
.
Советую попробовать, чтро будет, если справа

(тогда убывает), что будет, если справа стоят постоянные

.
А можете подсказать, как это сделать? Итак, рассмотрим

На занятиях по УМФ мы в таких случаях либо пытались разделить переменные, решали задачу Штурма-Лиувилля, а потом произносили заклинание под названием теорема Стеклова, либо, скажем, находили функцию Грина соответствующего оператора, после чего уже легко получалось решение. У меня инстинктивно есть желание попытаться разделить переменные

так что

Беря производную по

, получаем
![$$\frac{(T' + t T'') T - t (T')^2}{T^2} - \left[h'(t) t + h(t)\right] \frac{R''}{R} = 0 \implies \frac{R''}{R} = \lambda.$$ $$\frac{(T' + t T'') T - t (T')^2}{T^2} - \left[h'(t) t + h(t)\right] \frac{R''}{R} = 0 \implies \frac{R''}{R} = \lambda.$$](https://dxdy-03.korotkov.co.uk/f/e/f/0/ef0c2f566080622caf8738bbab9c5f5b82.png)
С другой стороны, подставляя это в исходное уравнение, имеем

откуда

Но эта система уравнений, насколько я могу судить, не имеет решений: у первого уравнения решения экспоненциальные, а у второго -- полиномиальные. Отсюда я заключаю, что метод разделения переменных тут, видимо, не работает, так что надо действовать как-то иначе. Или всё вышенаписнное вообще чушь?
Я люблю обозначать решения через

, т.ч. буду этому следовать, и предположу, что

, и нас интересует поведение при

(Вы стыдливо замолчали когда решение должно затухать), и что
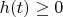
(по причине, что иначе задача будет плохо поставлена в положительном направлении времени).
Да, всё именно так. Вообще говоря, хотелось бы даже скорее найти какое-то характерное время затухания решения

. Честно сказать, я думал, что мало ли тут как-то умно можно переменные, например, разделить, получить какую-то хитрую задачу Штурма-Лиувилля, найти СЗ соответствующего оператора, увидеть, что временная часть затухает, и рассмотреть, как именно она это делает.
Если мы сможем оценить это сверху через
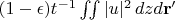
, что будет, например, если

,

или если

(

нормы), то все в порядке. Если нет, то надо думать... ответа я не знаю
Это надо будет подумать и посмотреть. Просто функции

,

заданы весьма условно, если честно: из численных результатов можно выцарапать, как они выглядят, как себя примерно ведут прикинуть, но вот динамику их нормы в смысле

я не смотрел.
А вот какая вещь стала интересна. А из каких-то общих соображений нельзя оценить характерное время затухания

без решения задачи? В том числе в более сложном случае, когда правой частью не пренебрегаем? Если уравнение в какой-то момент
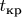
"лопается", но

, то и бог бы с ним, честно говоря: из некоторых физических соображений заранее известно, что начиная с некоторого (неизвестного мне) момента уравнение всё равно не способно адекватно описывать физику процесса.
(Оффтоп)
Умножая это уравнение на

и интегрируя по пространственным переменным, мы получим слева

Здесь явно очепятка: квадрат внутри

явно лишний.



