Тема
post1459672.html#p1459672 еще раз исправлена и дополнена.
The main goal of this paper is to compare properties of electrostatic models in special plane-layered inhomogeneous media, where

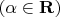
,
and properties of relevant electrostatic models in special axially symmetric (sometimes called "cylindrically layered") inhomogeneous media, where
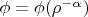
,
using analytic and geometric tools of generalized hyperbolic and axial-hyperbolic non-Euclidean modifications of the system
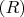
.
In Section 2, we recall basic notations of modified quaternionic analysis in

and relevant properties of electrostatic models.
In Section 3, we present generalized hyperbolic non-Euclidean modification of the system
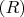
and implement new class of

-hyperbolic harmonic potentials in Cartesian coordinates using Bessel functions.
Applied properties of Vekua-type systems related to hyperbolic function theory are considered.
In Section 4, we present generalized axial-hyperbolic non-euclidean modification of the system
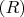
and implement new class of

-axial-hyperbolic harmonic potentials in cylindrical coordinates using Bessel functions.
Criterion of joint class of

-hyperbolic harmonic and

-axial-hyperbolic harmonic potentials is formulated.
In Section 5, we present generalized bi-hyperbolic non-Euclidean modification of the system
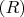
in the context of generalized bi-axially symmetric potential theory.
We implement new class of
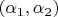
-bi-hyperbolic harmonic potentials in Cartesian coordinates in comparison with class of

-hyperbolic harmonic potentials.
Criterion of joint class of
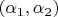
-bi-hyperbolic harmonic and
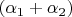
-hyperbolic harmonic potentials is formulated.
In Section 6, we focus on specifics of meridional electrostatic fields in axially symmetric inhomogeneous media.
Geometric properties of the so-called

-meridional mappings of the second kind are studied.
The Fueter holomorphic potential is presented as an extension of the complex potential in the context of GASPT.
In Section 7, we focus on geometric properties of harmonic analogues of

-meridional mappings of the second kind.
In Section 8, we consider a fairly wide range of meridional electrostatic models, described by the one-sided and two-sided reduced quaternionic Laplace-Fueter transforms of classical real-valued originals.
In particular, meridional electrostatic model, described by the Euler's Gamma function of the reduced quaternionic argument, is explicitly demonstrated.
Meridional electrostatic models, described by the reduced quaternionic Fourier-Fueter cosine, sine and exponential transforms, are demonstrated in the context of GASPT.
In Section 9, we consider physical and geometric aspects of electrostatic fields in inhomogeneous anisotropic media.
New generalized Riemannian modification of the system (R) is initiated.
Основной результат сформулирован в
Theorem 6.11 (On roots in the framework of the Fueter holomorphic potential in electrostatics)
https://arxiv.org/pdf/1904.08299v5.pdfТеорема позволяет расширить метод комплексного потенциала для применения в области меридиональных электростатических полей в некоторых неоднородных средах.
Все решения при этом находятся в рамках класса функций редуцированной кватернионной переменной, называемых радиально голоморфными.
Более общую формулировку современных проблем, возникающих при исследовании меридиональных полей в неоднородных средах, можно видеть в
Theorem 6.1 (On roots of the characteristic equation in case of meridional electrostatic fields)
Если что-то еще не так, пожалуйста, сообщите.