На школьном уровне — графически. Например, для неравенства

строим на одном чертеже графики функций

и

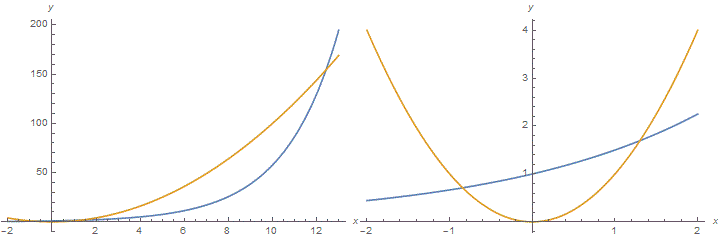
и смотрим, где они пересекаются (первые два графика). Можно также построить график функции

(последние два графика). Чтобы строить графики осмысленно, надо знать свойства показательной и степенной функций. По графикам можно приближённо найти координаты точек пересечения, а потом уточнить их, вычисляя значения функций на калькуляторе или компьютере.
Если абсциссы точек пересечения графиков слева направо обозначить

,

,

, то решение неравенства имеет вид

(или в виде совокупности неравенств

и

). Приближённые значения корней:

,

,

.
Вложение:
 Exp12.gif [ 7.04 Кб | Просмотров: 1405 ]
Exp12.gif [ 7.04 Кб | Просмотров: 1405 ]
Вложение:
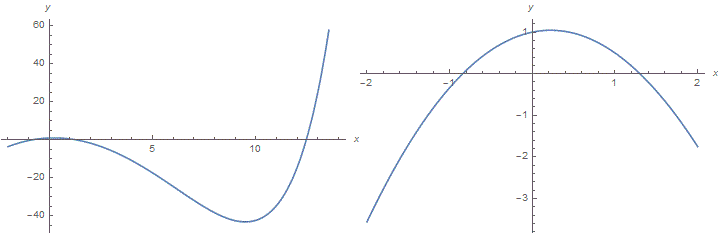 Exp34.gif [ 5.25 Кб | Просмотров: 1405 ]
Exp34.gif [ 5.25 Кб | Просмотров: 1405 ]
Но интересует не наглядная демонстрация решения, а вывод формулы.
Вы не поняли? На школьном уровне нет никакой формулы, а тем более — её вывода. При желании можно просто придумать какую-нибудь "нешкольную" функцию и обозначение для неё, и писать какие-нибудь формулы с этим обозначением. Легче Вам от этого не будет, поскольку вычислять-то придётся всё равно численными методами, которые в школе не изучают. Даже и для школьных функций: тангенс и арктангенс вполне школьные функции, но много ли найдётся школьников, которые смогут вычислить

или

?



