О. Отлично. Ну и проделайте эту операцию шесть раз, ровно как в условиях задачи перечислено.
Какие 6 раз? Не понимаю это место.
Можно так: найдите середину

отрезка

Найдите середину

отрезка

Внимательно посмотрите на них.
А что значит "найти середину"? Если бы была задана система координат, то "найти точку" - это найти упорядоченный набор из

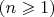
чисел. Но в задаче никакой системы координат не фигурирует. И вводить ее не надо.
Если принять, что у двух отрезков есть ровно по одной середине, и есть ровно одна точка пересечения, то утверждения выше эквивалентны.
Скорее всего да.
-----------------------------------
-----------------------------------
Смог я вроде бы доказать.
Итак, докажем, что

- середина

и

- середина отрезка

. Для произвольной точки

плоскости справедливо следующее:
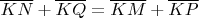
(доказывается тривиально). Выберем в качестве точки

точку

. Получим:

. Вектор

коллинеарен прямой

, а вектор

коллинеарен прямой

. Векторы равны тогда и только тогда, когда равны их модули и они сонаправлены (а следовательно коллинеарны). Если векторы

и

равны, то их длины обязаны быть нулевыми, т.к. в противном случае окажутся равными два ненулевых неколлинеарных вектора (т.к. прямые

и

не являются параллельными), чего быть не может. Получили, что
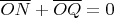
, следовательно
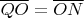
, следовательно

- середина отрезка

. Аналогично,

, следовательно

, следовательно

- середина отрезка

, чтд.
Но хотелось бы все же узнать, как должно выглядеть доказательство, о котором речь шла выше, и которое я не смог воспроизвести. Вот я в упор не вижу, как с помощью вот этого утверждения
Т.е. если дан вектор

и

- произвольная точка плоскости, а

- середина

, то
![$\overline{OC} = \frac{1}{2} [\overline{OA} + \overline{OB}]$ $\overline{OC} = \frac{1}{2} [\overline{OA} + \overline{OB}]$](https://dxdy-01.korotkov.co.uk/f/4/c/b/4cb347ae576bb711f777889b0ac33a4b82.png)
доказать эту теорему.



