Ну нотация-то простая: вначале мы разрешаем себе писать

для точки, полученной из

переносом на

, потом

для

, потом
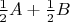
для

(или
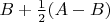
) — и потом остаётся лишь убедиться, что назревающие подозрения действительно верны, и развязать себе руки.
-- Пт мар 13, 2020 16:48:55 --Она ещё более естественна, если прийти к аффинному пространству как подмногообразию линейного, потому что векторы-то можно всегда складывать и умножать на скаляры, и остаётся лишь установить то простое правило, определяющее, даёт ли линейная комбинация из населяющих то подмногообразие радиус-векторов радиус-вектор (или же даёт вектор, который можно получить вычитанием одного радиус-вектора из другого, или же даёт что-то, не являющееся ни тем, ни тем).