О, ту вещь пропустил. Я бы сказал, не стоит обозначать две разные функции как

. Левая

в формуле — это

, а правая

—
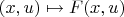
, ну или просто

— и в вычислении производной я бы первую

оставил как есть, раз никакого короткого обозначения у неё не получится, а вместо второй написал бы законную

, раз уж ей уже дали имя. Лучше бы им обеим дали имена как следует, а не только в виде букв, обозначающих выражения или переменные (как в случае с

).
Спасибо! Я до этого как раз сам додумался, а тут Вы подтвердили.
Но кстати говоря помнится, что классически вместо левого вхождения
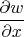
вроде рекомендуется писать

, именно чтобы не путать, где мы взяли частную производную, а где взяли пропорциональную

часть
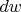
. Хотя это наверно не лучшее обозначение, потому что вот делением дифференциалов это как раз не будет — кроме редкого случая, когда большая функция в итоге имеет лишь один аргумент, по которому и дифференцируется, а в этой теме например их два.
Именно это меня подвело и смутило. Я в учебнике встретил формулу:

Потом начал переносить на свой случай и пришел к странной формуле, над которой долго ломал голову.

Хотя на деле все трудности не в каких-нибудь тайных закоулках производной композиции функций, а в лени авторов курса написать лишнюю пару букв и слов.
Где ж найти такого автора, который в состоянии охватить все возможные вывихи человеческого сознания?
