Подскажите, пожалуйста, как правильно перевести на русский два предложения:
Let

be the number of

-cliques,

, in a random permutation graph

with

vertices and
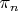
is the corresponding permutation representation in

.

and

is the number of edges in

which is just the number of inversions in

, denoted by

.
Какой именно смысл приобретают

и

? То есть не очень понятно, что в этом случае это за числа "клики". Могли бы вы пояснить, если можно с примером. Спасибо.
Мой перевод:
Пусть

число

-клики,

, в случайном графе перестановок

, имеющим

вершин, и
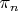
есть соответствующие представление перестановки в

.

и

число граней графа

, которое есть число инверсий в

, обозначаемое, как




