
- гладкая кривая.

при
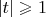
.
Точки самопересечения

- простые и трансверсальные.
Знак точки самопересечения

определяется так: если

- правоориентирован, то

, левоориентирован, то

.
Тогда
![$f':[0,1]\to \mathbb{R}^2\backslash \left\lbrace 0 \right\rbrace$ $f':[0,1]\to \mathbb{R}^2\backslash \left\lbrace 0 \right\rbrace$](https://dxdy-03.korotkov.co.uk/f/2/b/c/2bcb5418c22144a2009803ed7fe9a4fa82.png)
- кривая, которая начинается и заканчивается в точке

, её класс в

называется индексом

.
Доказать
a) число точек самопересечения

конечно;
b) теорему Уитни: сумма

всех точек самопересечения равна индексу кривой.
Подсказка: используйте
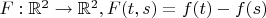
Под а), вроде, решил.
Пусть

Тогда

, т.к. точки пересечения трансверсальны. По теореме об обратной функции получается, что у каждой точки пересечения есть окрестность, в которой нет других точек пересечения, то есть каждая точка пересечения изолированна.
Рассмотрим

на компакте
![$[-1;1]$ $[-1;1]$](https://dxdy-01.korotkov.co.uk/f/8/2/4/824138638ae0b24e5665173857dfe11e82.png)
. Покроем его интервалами с точками пересечения и интервалами между ними, выберем конечное покрытие. Значит и точек самопересечения конечное число.
Верное решение?
Под b) сложнее.
Во-первых, почему

определяется на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
, а не на
![$[-1;1]$ $[-1;1]$](https://dxdy-01.korotkov.co.uk/f/8/2/4/824138638ae0b24e5665173857dfe11e82.png)
?
Что имею


можно прогомотопировать

. Индекс

станет честным классом отображения в окружность. Вот как-то связать не получается. Что можно сделать?



