Я, кажется, продвинулся в решении.
Так как третьих гомологий у тора и сферы нет, то элементами вторых гомологий будут двумерные циклы.
Рассмотрим тор как квадрат
![$[0,1]\times [0,1]$ $[0,1]\times [0,1]$](https://dxdy-04.korotkov.co.uk/f/7/0/7/70719255eeec7e456629f50f69bce88a82.png)
со склейкой сторон. Диагональю разобьём его на два треугольника

. В

отправим один двумерный симплекс, в

- второй. Отправим так, чтобы у цепи

была нулевая граница. Получим двумерный цикл. Не могу только строго показать, что этот цикл будет именно образующей

. Как это можно сделать?
Но для задачи с определителем это и не надо, так как гомоморфизм

достаточно задать на любом элементе (не обязательно на образующей). Вроде, с отображениями между торами решил, получается.
Далее, для сферы возьму тот же квадрат и его границу стяну в точку. Получу двумерный цикл.
Доказать, что для любого непрерывного

отображение
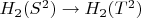
- нулевое.
Здесь мне надо показать, что любое непрерывное отображение двумерного цикла сферы нельзя перевести в цикл тора. Здесь есть идея использовать теорему о клеточной аппроксимации (её нам доказывали в предыдущем курсе). То есть надо показать, что не существует клеточного отображения из сферы в тор, переводящего цикл сферы в цикл тора.
Беру сферу как объединение нульмерной и двумерной клеток. А тор - нульмерная, две одномерных и одна двумерная.
При клеточном отображении из сферы в тор нульмерная клетка переходит в нульмерную, а двумерная должна перейти в объединение двух одномерных и двумерной у тора. Почему так не может быть? Ведь образ открытого не обязан быть открытым.
Для отображения из тора в сферу проще. Нульмерная и одномерные клетки тора переходят в нульмерную клетку сферы, а двумерная в двумерную. Для того, чтобы это был изоморфизм, мне надо показать, что указанные циклы - образующие вторых гомологий. Как это сделать?
И где я что-то, может, упустил важное?



