Потому что я искусственно задал режим на постоянном токе, который через конденсатор не течет.
Стало понятнее, что токов

и

не будет, но всё равно не понимаю почему в таком случае

, если чисто интуитивно, то, кажется, что это не так.
Из тех, что через резистор

ток течет из земли в узел b.
Он по другому протекать не может при постоянном токе ввиду того, что потенциал

не может быть больше потенциала

?
Это не обязательно происходит без колебаний и не обязательно они затухающие, так как есть активный элемент

.
Не очень представляю по какому закону растет потенциал

, а потому не очень понимаю за счет чего будут происходить колебания. В момент времени

имеем

, затем

растет по какому-то закону, следовательно, разность

. Причем активный элемент не может вроде бы повлиять, так как

сам на него влияет, например, в момент
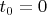
управляющее напряжение

отключает источник

.
-- 20.10.2019, 23:51 --Честно говоря вышеописанную систему уравнений не удалось мне решить.
Между прочим, это обычная система линейных дифференциальных уравнений.
Ну преобразовал, а вот преобразованную систему не назвал бы обычной, так как не ясно что и куда тут подставлять.

А найдите-ка установившийся режим работы схемы в предположении отсутствия возбуждения.
С радостью, только подскажите, что конкретно требуется занулить или что требуется сделать дабы отбросить возбуждение.



