Emergency, мне самому не нравится такая формулировка, ни направления токов не задано, ни потенциалы не подписаны хотя бы формально, по схеме видно, что она нарисована в каком-то сапр и всё. Задача у меня несколько в другом, но начало я переписал один в один. Дальше такой текст.
Написать программу на C/C++, которая вычисляет напряжение на выходе

в заданный момент времени

и с ее помощью найти напряжение на выходе

в момент времени

нс. Подсказка для самопроверки и отладки: напряжение на выходе

в момент

нс приблизительно равно

В.
Это одно из тестовых заданий на программиста, я глазами пробежался по задачам, смутила только эта, т.к. формулы для потенциала то нет. Соответственно мне важно понять, есть ли она вообще тут, хватает ли данных, либо нужен какой-то другой подход.
-- 19.10.2019, 18:23 -- Насколько я смог понять, требуется рассмотреть переходной процесс и найти реакцию схемы (напряжение на выходе) при скачкообразном увеличении напряжения на входе от 0 до 1 вольта.
Это так? Или задача в другом?
Думаю задача именно в этом.
-- 19.10.2019, 18:29 --Как это ничего? А начальные условия?
Согласен, начальные условия есть — в момент
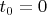
ток через катушку не проходит, то есть

, а значит и

и изменения никакого нет

. Только дальше то что делать?