Написал ликбез по нестандартному анализу

[george66]

Оцените, покритикуйте
https://mega.nz/#!a44XgSCZ!lrG-h5tHEpx1 ... 2jMaurxYPs
Это первая версия, готов её расширять, но полнометражный учебник писать не буду, нестандартный анализ меня не настолько вдохновляет. Могут быть ляпы и ляпчики. Если что-то непонятно, не стесняйтесь говорить.

[arseniiv]

george66
Вот наконец-то я долез до чтения. Пока ощущается довольно понятным для незнакомых с матлогикой.

Что бы я, если бы был автором, поменял:

(незначительное)

Цитата:

Итого, терм $1+2$ есть $1+(1+1)$ <…>
<…> функции и отношения на множестве действительных чисел.

Этот кусок я бы отделил небольшими вертикальными интервалами от текста перед и после, т. к. он на время прерывает перечисление «индуктивных частей языка». Вообще я бы придал всем абзацам или левый отступ первой строки, или интервалы между.

(незначительное)

Цитата:

Атомарные формулы имеют вид <…>

Не уверен, что не знакомым с матлогикой так просто понять, что формулы обозначают высказывания, хотя прям сразу в этом же куске их примеры. Может потребоваться отступление на одно предложение, вот про термы выше написано «выражения».

(незначительное)

Цитата:

Замкнутые формулы – это такие, в которых нет свободных переменных (параметров, <1> все переменные связаны кванторами).

Запятую <1> я бы для прочности сделал точкой с запятой, а то она выглядит немного двусмысленной.

(незначительное)

Цитата:

Интервалы можно брать замкнутые, открытые, полуоткрытые в любую сторону и бесконечные в одну или обе стороны.

Не уверен в статистике, но может найтись достаточно людей, которые здесь проще восприняли промежутки вместо интервалов (которые они сочли бы открытыми промежутками). Хотя контекст, разумеется, достаточный чтобы понять.

(незначительное)

Цитата:

$Ind(A)$

А может быть $\mathrm{Ind}(A)$ или $\mathsf{Ind}(A)$.

(незначительное)

Цитата:

Содержательно, $p$ задаёт блок (порядок <2> блоков плотный без первого и последнего элемента)

В <2> я бы вставил «нестандартных». Стандартный блок-то первый.

(опечатка)

Цитата:

Если мы хотим что-то доказывать в логике второго порядка ( а не „брать все истинные формулы <…>

Лишний пробел после скобки.

(опечатка)

Цитата:

то $c \in {}^*(A - \{0\})$

Тут впервые (кажется) разность множеств записывается минусом, когда выше на той же странице она записывается через $\setminus$.

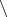
(незначительное)

Цитата:

$Fin$

(Аналогично $Ind(A)$ выше.)

(совсем незначительное)
Попадаются записи вида $\{a\ldots b\}$, где я бы поставил запятые вокруг многоточия.

Содержательно я не могу быть уверен в части про построение меры Лебега, потому что моей голове стало нехорошо, в остальном вроде никаких проблем.

-- Пн сен 23, 2019 02:21:28 --

Ах ещё да,

george66 в сообщении #1415155 писал(а):

готов её расширять

может, чуть раздуть место про плотный порядок нестандартных блоков натуральных чисел (или отослать): не сразу очевидно, почему $[c/2]$ и $2c$ не лежат в том же блоке что и $c$ (а $[(c+c')/2]$ — в блоке $c$ или $c'$; хотя тут очевиднее из-за симметрии: если лежит в одном, должно и в другом, но эти два блока не пересекаются).

-- Пн сен 23, 2019 02:22:55 --

Надеюсь, эти комментарии вам окажутся полезными. Если бы ваша книжка по категориям была бы размером в этот ликбез, я бы тоже её быстренько раскомментировал, но…

[george66]

Я книжку по категориям первоначально уложил в сто страниц, но её так раскомментировали, что пришлось браться всерьёз.

-- 23.09.2019, 02:39 --

Вообще, нестандартный анализ чем хорош - безумие теории множеств он преподносит явно. Люди, привыкшие к теории множеств, уже не замечают, что её делал сумасшедший. А вот вам Хрбачек и Нельсон (а то ещё Вопенка с AST) и Есенин-Вольпин с ними.

[ArshakA]

Здравствуйте, george66, вопрос по заметке. На 10 странице вы пишите :

Цитата:

А вот множество обычных (стандартных) натуральных чисел не определимо. [..] Это не так удивительно, поскольку нестандартная модель специально так строилась, чтобы никакой формулой первого порядка нельзя было различить обычные числа от бесконечно больших.

Правильно ли я понимаю, что на практике это не создает проблем, потому что множество обычных натуральных чисел выделяется из гипервещественных средствами ZFC с помощью рекурсивного определения, например (корректность рекурсивного определения проверяется с помощью аксиомы о существовании образа функции) ?

[george66]

Если аксиоматизировать "нестандартную теорию множеств", там добавляют предикат $St$. Он выделяет стандартные элементы ($St(0),St(1),St(2)\ldots$). Тогда сохраняются, грубо говоря, формулы, не содержащие предиката $St$. Например, возьмём такую формулу
$\forall n\,(\neg n=0\Rightarrow\exists m\,(n=m+1))$
("перед каждым натуральным числом, не равным нулю, есть предшественник"). Предполагается, что переменные $n,m$ пробегают по гипернатуральным числам. Формула не содержит предиката $St$. Теперь возьмём соответствующее утверждение для стандартных натуральных чисел
$\forall^{St} n\,(\neg n=0\Rightarrow\exists^{St} m\,(n=m+1))$
Эта формула равносильна исходной, принцип переноса.
Следите за темой, через некоторое время выложу слегка исправленный вариант (нашёл две мелких опечатки). Могу также что-нибудь добавить или разъяснить, если есть пожелания.

[AndreyIos]

Скажите, пожалуйста, чем Ваш нестандартный анализ отличается от классического нестандартного анализа, изложенного в книге: В.А.Успенский. Что такое нестандартный анализ? - М.: Наука. Гл. ред. физ.-мат. лит., 1987, - 128 с.

[george66]

Ничем, он общий. Я ничего не придумывал. У меня больше подробностей.

[AndreyIos]

Спасибо за ответ. Скажите, пожалуйста на кого рассчитано Ваше пособие? Является ли оно учебным?

[george66]

Это ликбез для русскоязычных математиков, невежественных и неблагодарных. Книжка Успенского для продвинутых школьников. Книжка Дэвиса по замыслу учебник, но не очень понятный. Гордон-Кусраев-Кутателадзе скорее большой обзор. Учиться и по тому и по другому трудно. Цель ликбеза - сделать возможным чтение этих книг, а также англоязычных, которых много.

[g______d]

george66 в сообщении #1420947 писал(а):

Цель ликбеза - сделать возможным чтение этих книг, а также англоязычных, которых много.

Спасибо. Я когда-то ходил на спецкурс по нестандартному анализу и сдавал экзамен (хотя это была практически ортогональная тематика, посвящённая "конкретной реализации" через ультрафильтры). Если бы был доступен этот текст тогда, было бы намного проще.

[AndreyIos]

george66 в сообщении #1420947 писал(а):

Это ликбез для русскоязычных математиков, невежественных и неблагодарных. Книжка Успенского для продвинутых школьников. Книжка Дэвиса по замыслу учебник, но не очень понятный. Гордон-Кусраев-Кутателадзе скорее большой обзор. Учиться и по тому и по другому трудно. Цель ликбеза - сделать возможным чтение этих книг, а также англоязычных, которых много.

Большое спасибо за Ваши благородные устремления. Искренне желаю удачи.