Получается ядро первой (справа) = образ второй, т.е.

Как раз обязательно
Значит, ядро второй, оно же образ третьей, также

.
Но ведь, таким же образом, ядро третьей -

. Верно?
А значит, и образ четвёртой

.
Полезно доказать такое утверждение: если абелева группа содержит подгруппу, изоморфную

, а фактор по этой подгруппе изоморфен

, то вся группа изоморфна

.
Вот тут оно и полезно. Получаем

. Правильно?
Выписать гомоморфизмы между нулевыми группами гомологий
Здесь, получается, можно без этого обойтись?
Но всё-таки. Третья стрелка переводит элемент (1,0) в (1,1) (т.к. переводит первую окружность в оба цилиндра), и элемент (0,1) - в (1,1). Матрица

Ранг у неё один, значит в образе третьей стрелки будет одно циклическое слагаемое. Поэтому образ

. Верные рассуждения?
-- 06.10.2019, 09:17 --Вообще, вы, кажется, путаетесь в алгебре, конкретно в абелевых группах
Да, сталкиваюсь. Поэтому и стараюсь разобраться. Причем, те утверждения, что Вы назвали, знаю. Винберга читал. Но вот здесь вопросы возникают.
Например.
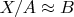
. Означает ли это, что
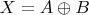
?
Полезно доказать такое утверждение: если абелева группа содержит подгруппу, изоморфную

, а фактор по этой подгруппе изоморфен

, то вся группа изоморфна

.
Это, наверное, доказывается прямым построением изоморфизма? Или как-то проще можно?