epros, спасибо за ответ.
Я привык называть законом контрапозиции
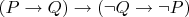
. Потому что это закон не только в классической логике, но и, например, в конструктивной. Обратное:
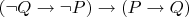
- в конструктивной логике не всегда верно, а потому так не называется.
Вас понял.
Надо сказать, что такие доказательства малоинтересны. Если Вы уж решились опираться на двузначность логики, то зачем эти пляски с бубнами? Просто подставьте вместо всех пропозициональных переменных все возможные комбинации логических значений и убедитесь, что тавтология всегда истинна.
То есть подобного вида утверждения в случае, когда я принимаю фактически за аксиомы способы работы с высказываниями посредством логических связок, тоже становятся аксиомами?
Просто именно такие доказательства корректности предоставляются в книге. Но более краткие. И я хотел для себя разобрать эти места поглубже.
beroal, спасибо за ответ.
Если я правильно понял, вы с помощью доказательства от противного хотите доказать импликацию.
Нет, я хочу обосновать корректность применения метода доказательства от противного в случае, когда мое утверждение имеет вид импликации. Ведь повсеместно в анализе и алгебре приходится от противного идти доказывая утверждения вида

.
arseniiv, спасибо за ответ.
Вот как раз с общей схемой у меня вопросов нет. Пусть имеется утверждение.

. Предположим, что оно неверно, то есть верно

. Придём к противоречию, то есть получим, что
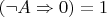
. Но тогда

, а значит

.
То есть когда я разбираю доказательство общего вида, например, утверждение об иррациональности

, проблем у меня нет.
И тогда я решил применить этот метод к частному типу высказываний, которые так часто приходится доказывать.
Приведу пример.
Утверждение.Пусть

- векторное пространство,

- поле.
Тогда если

.
Докажем это утверждение от противного.
У меня есть

.
Есть

.
Нужно доказать, что

.
Если я правильно понимаю, то я считаю

уже нам данным, то есть

.
Тогда предположим, что
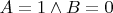
. И все докажется.
Заскок у меня тут. Ведь в любом случае, всегда из истины ложь следовать не может. Значит тот факт что

ложен еще до попытки доказательства его не истинности?