А, понятно. Строки и столбцы - это как договоримся. Договорились, что столбцы - это векторы. Главное, что базис векторов по определению находится в

. А дуальный базис ковекторов по определению находится в
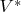
.
При преобразованиях базиса

компоненты векторов преобразуются обратно своему базису

. И компоненты ковекторов преобразуются обратно своему базису
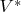
, т.е. внутренние свойства пространств

и
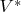
совершенно одинаковые. И проекции ковекторов на базис
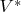
выполняются совершенно так же, как проекции векторов на базис

. Только преобразования их базисов всегда связаны обратной зависимостью.
Можно сказать так: при преобразованиях базиса компоненты векторов преобразуются обратно своему базису

, а компоненты ковекторов - обратно своему базису
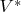
. Но говорят так: компоненты векторов преобразуются обратно базису

, а компоненты ковекторов - так же, как базис

. Это одно и то же, но немного маскирует равноправие векторов и ковекторов.
Еще я понял, что линейный оператор, билинейная форма и тензор (2,0) - все это не имеет прямого отношения к связи векторов и ковекторов. Переход от вектора к ковекторам и обратно происходит по определению только при помощи метрического тензора, а не просто какого попало линейного преобразования. Кроме метрического тензора ничто другое не может "поднимать и опускать индексы", т.е. преобразовывать векторы в ковекторы и наоборот.
Линейный оператор, т.е. тензор (1,1), билинейная форма, т.е. тензор (0,2) и тензор (2,0) называются по разному только из-за разного закона преобразования их компонент (который получается разным потому, что матрицы этих объектов получены тензорным перемножением либо векторов, либо ковекторов, либо одних с другими), а не из-за того, что они выполняют разные математические операции.