Однажды мне понадобилось аналитически сосчитать определитель матрицы, слабо отличающейся от единичной. И сочинил я следующее представление

где величины

вычисляются рекуррентно
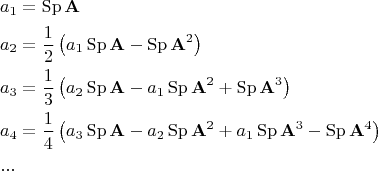
Ряд

на самом деле содержит конечное число слагаемых, так как для произвольной матрицы размера

все

-шки обнуляются начиная по крайней мере с

(или ещё раньше). При этом сама матрица наверняка удовлетворяет уравнению
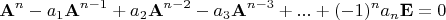
или ещё какому-то, меньшей степени, из списка

Доказывать всё это я тогда не стал. Так, проверил правильность для разумных размеров и зафиксировал в памяти как "рецепт". Не то чтобы была какая-то реальная надобность в доказательстве для произвольных

(при ручном труде терпение лопается уже на вполне скромных габаритах), но может есть элементарно простой способ это сделать? Я бы лучше запомнил такой способ, вместо "рецепта".



