Проблема только в том, что нельзя изучать математику по Википедии
Согласен. Определение из Википедии общепринятое, потому его и привел. Читаю Зорича. Заглядывал в Фихтенгольца. Определения имхо у обоих авторов недостаточно общие (особенно у Фихтенгольца).
3. Тут два варианта: либо вы дошли до конца — и у вас есть удобный вам матаппарат; не смогли докаазать какую-нить из теорем — и у вас есть ответ, чем плохо ваше определение.
Предлагаете проверять все теоремы из Де Брейна?

А если серьезно, то ровно так я и делаю по возможности (я не про Де Брейна, а про те теоремы, которые в учебнике)
1. Определяете о малое как вам удобно.
Я хочу сформулировать такое определение, которое подходило бы для любых двух функций
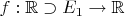
и

, какие бы области определения

и

у них ни были (пусть хоть

). Единственное требование для функций - чтобы точка

(в которой мы сравниваем асимптотику) была предельной как для

, так и для

. Ну и понятно, что это определение должно обобщать существующие и не противоречить им. Я думал добавить требование локального совпадения областей определения этих функций в некоторой окрестности точки

, но мне это тоже не нравится, т.к. в таком случае не получиться сравнить функции

и

, где первая определена на

, a вторая на

и те, которые предложил
ewert.
Если немного отвлечься от определений и подумать над интуитивным смыслом о малого - что мы от него хотим? Имхо мы хотим, чтобы запись
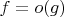
означала, что функция

"пренебрежимая", "бесконечно малая по сравнению с"

. Одно определение ставит в основу сравнения двух функций поведение их отношения. Другое определение ставит в основу представление одной функции как произведение другой и бесконечно малой. В обоих случаях области определения функций должны хотя бы локально совпадать. Но что если в основу сравнения этих двух функций ставить не их отношение и не их представление, а их колебательные функции. Возьмем функцию

. Каждой

поставим в соответствие колебание функции

на проколотой

-окрестность точки

, т.е. величину
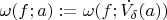
. Тоже самое сделаем с функцией

. Каждая из этих функций

и

породит свою колебательную функцию. Может быть есть смысл сравнивать асимптотику функций

и

не напрямую через эти самые функции, а сравнивая поведение их колебательных функций в окрестности нуля? Колебательные функции очень красивые - они определены на

и монотонно неубывают. Будем писать
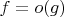
, если колебательная функция, порожденная функцией

, "затухает" "быстрее", чем колебательная функция, порожденная функцией

. Можно ли развить теорию с такой точки зрения?