А процитированный Вами текст может быть оценен только как левый уклонизм в теории приближенных вычислений и должен быть вамаран цензурой из учебника!
Тогда вымарать придется и Фихтенгольца: когда он рассматривает вопрос вычисления

при

измеренном с погрешностью

в параграфе "108. Применение дифференциалов при оценке погрешностей", он пишет
Цитата:
...Ввиду малой величины этих погрешностей, полагают

т.е. заменяют приращение дифференциалом. Пусть
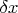
будет максимальной абсолютной погрешностью величины

(в обычных условиях подобная граница погрешности при измерении известна). Тогда, очевидно, за максимальную абсолютную погрешность (границу погрешности) для

можно принять

В Демидовиче, Мароне присутствует марафет

они говорят о "предельных" погрешностях, так что обошлось не без попытки соблюсти математический аккурат.



