Вопрос про константу кислотности

[MarEagan]

Согласно правилу Полинга константу кислотности кислородсодержащей кислоты по первой стадии можно найти по формуле $pK_a = 5n - 8$, вопрос в том что из себя представляет число 8.

[Pphantom]

Эмпирическое значение. И, кажется, вы знак перепутали.

P.S. И формулы надо правильно набирать. Выше я это поправил сам.

[MarEagan]

Хм, может я что-то недопонимаю, но должно же оно чему то соответствовать?

[madschumacher]

MarEagan в сообщении #1410701 писал(а):

Хм, может я что-то недопонимаю, но должно же оно чему то соответствовать?

Оно соответствует сложному и огромному выражению, которое непонятно выглядит, как его посчитать, и что оно значит, но которое легко оценить из эксперимента.

[MarEagan]

Можете название выражения подсказать?

[Pphantom]

MarEagan, на форуме принято обращаться к собеседникам на "вы".

[MarEagan]

Извиняюсь, я здесь недавно.

[aitap]

Под эмпирическим значением понимается следующее: Полинг взял множество имеющихся на тот момент данных о константах для оксокислот (сейчас они доступны в таблицах вроде этой) и провёл их статистическую обработку:

(код на R)

pKa <- read.table(text =
'HClO4   -10
H2SO3   1.9
H2SO4   -3
H3PO4   2.12
HNO3   -1.3
HNO2   3.29
H2CrO4   -.98
H3BO3   9.23
H3AsO4   2.22
H3AsO3   9.22
H2BeO2   3.7
HOBr   8.7
HOCl   7.53
HClO2   2.0
HClO3   -1
H2CO3   6.37
HCrO4   6.50
H2GeO3   8.59
HOI   11
HIO3   .8
H5IO6   1.64
HMnO4   -2.25
H3PO3   2
HReO4   -1.25
H2SeO3   2.6
HSeO3   8.32
HSeO4   2
H3SiO3   10
H2SO3   1.9
H2SO4   -3
HSO3   7.21
HSbO2   11
H2CrO4   .74
H3PO4   2.12
H3AuO3   13.3
H3GaO3   10.32
H5IO6   3.29', col.names = c('formula', 'pKa'), stringsAsFactors = F)
library(stringr)
library(magrittr)
pKa$H <- pKa$formula %>% str_match('(?<=H)\\d+') %>% as.numeric() %>% ifelse(is.na(.), 1, .)
pKa$O <- pKa$formula %>% str_match('(?<=O)\\d+') %>% as.numeric() %>% ifelse(is.na(.), 1, .)
pKa$n <- with(pKa, O - H)

plot(pKa ~ n, pKa)

library(MASS)
x <- rlm(pKa ~ n, pKa)
abline(coef(x))
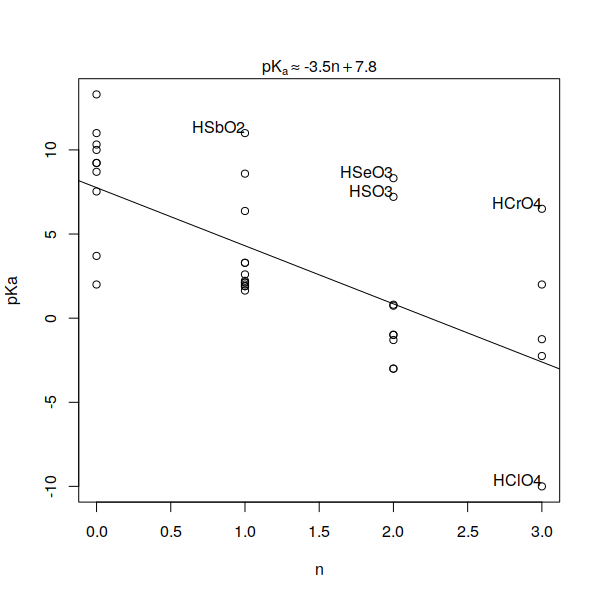
mtext(bquote(pK[a] %~~% .(signif(coef(x)[2], 2))*n + .(signif(coef(x)[1], 2))))

outl <- abs(resid(x)) > quantile(resid(x), .9)
text(pKa[outl, c('n', 'pKa')], labels = pKa[outl, 'formula'], adj = c(1,0))

На графике $ pK_a $ от $n$ видно, что наклон, действительно, близок к $-5$, а пересечение с $ n = 0 $, действительно, проходит в точке, близкой к $pK_a = 8$:

[madschumacher]

MarEagan в сообщении #1410703 писал(а):

Можете название выражения подсказать?

По-сути, это энергия Гиббса (с точностью до множителя).

[MarEagan]

Спасибо
Pphantom
aitap
madschumacher