Пусть корни уравнения:

,

и

(извините, я здесь

переобозначил, но я больше к исходному уравнению не вернусь). По теореме Виета

,
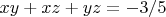
. Когда я загнал эту систему в WolframAlpha, она мне выдала:

Значит,

, где

. Преобразуем:
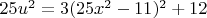
или, переобозначив,

. Приведя рациональные дроби

и

к общему знаменателю

, имеем уравнение в
натуральных числах:

(извините ещё раз, я тут опять переобозначил дроби

и

их натуральными числителями). Вспоминаем теорему Ферма—Эйлера: в разложении числа справа на простые множители тройка входит в нечётной степени, а слева — в чётной степени. Значит, уравнение решения не имеет.
Но, может быть, я где-то ошибся.



