Хаос в динамической системе - это когда система неустойчива к изменению начальных условий. То есть, если мы зададим некие начальные данные (координаты и скорости) и проследим эволюцию системы, а потом начальные данные чуть изменим - эволюция получается другой (траектории из близких точек в фазовом пространстве со временем разбегаются все дальше и дальше). Система из твердых шариков (даже небольшого их количества) таким свойством обладает в полной мере.
Не особо понял...
1) Во первых, в каком смысле динамической? В том смысле что оно изменяется со временем, или в том смысле что там не кинематика а динамика, то есть есть некоторые силы которые зависят от самого движения, например сила кулона между шариками?
2) В каком смысле неустойчивость в данной системе? У нас есть шарики в модели, допустим штук двадцать, мы знаем все что нужно, мы знаем характер движения — траектории движения это прямые в пространстве, удары шариков абсолютно упругие, без скольжения или деформации. Мы посмотрели эволюцию системы при одних начальных условиях, посмотрели при других, все абсолютно детерменировано, никакой случайности нету.
Какой же это хаос если мы знаем насколько изменится поведения системы при сколь угодно малых изменениях начальных условий на сколь угодно большой срок вперед? Допустим у нас есть плоскость в пронстранстве и частица, допустим у нас есть какой-то центр на плоскости, допустим с этого центру можно провести прямую к частице.
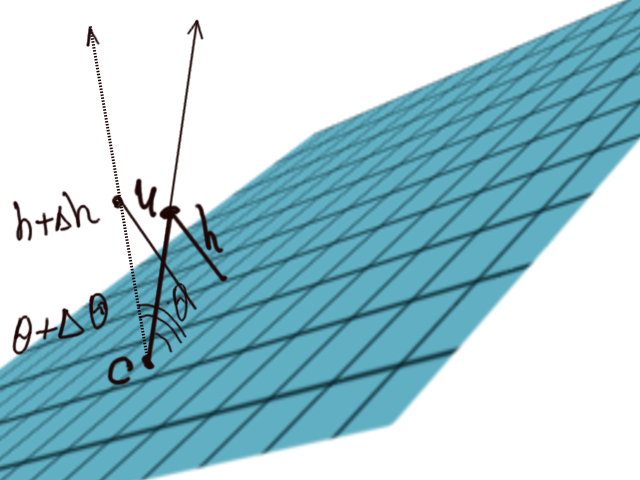
Частица движется с постоянной скоростью по этой прямой, мы можем однозначно проследить зависимость расстояния частицы до плоскости

от угла

в какой-то момент времени. Допустим тета изменилось не сильно, на

, тогда и расстояние

изменится не сильно, а я скажу а давайте выберем что достаточно много времени прошло, тогда расстояние измениться сильно. Это тоже будет хаотическая система в которой при малых изменениях два будущих развития все далее и далее одно от одного при прошествии все большего и большего времени? В таком смысле все системы хаотические если взять достаточно много времени, кроме статических конечно же.
Совсем другое дело на рисунке втором, там шариков слишком много, соответственно мы теоретически можем, но практически не можем
предсказать поведения каждого с этих шариков, и как результат с огромной степенью точности можно считать что движение любого шарика с этой системы есть хаотическое движение,
абсолютно непредсказуемое. Например у нас есть порядка десять в двадцать третьей абсолютно одинаковых шариков, очень много.
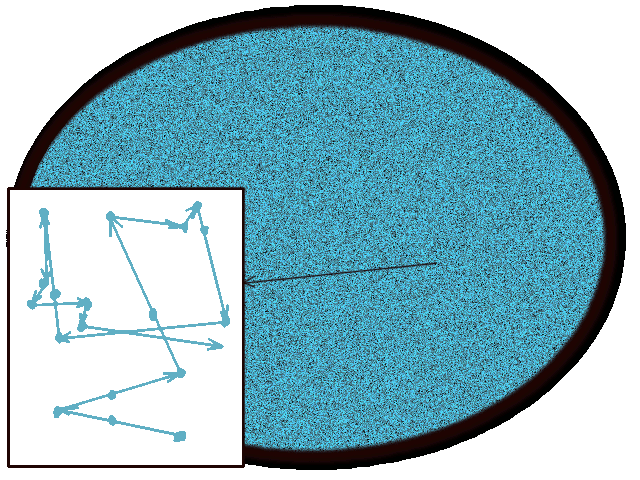
Мы берем, включаем "Глаз Бога", и смотрим за поведениям одного из шариков, забываем, не видим всех остальных шариков, и даже стенки. Вот я всегда считал вся классическая термодинамика построенная на том что поведения этого шарика, его движение, мы предсказать не можем, с огроменной точностью можем сказать то что мы не можем предсказать! Мы не можем выделить никакой, как это, не знаю слова по русском, pattern в движении, оно в нашей модели
абсолютно хаотическое, или же случайное. Вот к этому словосочетание "включить хаос" подходит?