Ага, вроде, всё получилось.
Самая нижняя, гм, "парабола" похожа на то, что нужно. Она ограничена двумя функциями, определяемыми неявными соотношениями (как и раньше, всё выписывается явно, но неявно красивее и компактнее):

где

принимает два значения 0 и -1 (откуда и получаются две функции),

— главная ветвь функции Ламберта,

— вторая. Обе ветви сходятся в точке

. Посмотреть на это чудо можно
здесь.
Дополнение: тут я перемудрил, конечно. Нужно было выражать

через

, и получилось бы однозначное аналитическое выражение.
Внутри этой (выпуклой) области последовательность расходится, снаружи (здесь всё имеется в виду только внутри области

,
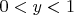
) сходится.
Понятно, что всё это симметрично отображается и в область
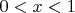
,

.
Правда, у меня есть один пробел.
Понятно, что всё упирается в решение уравнения

, где

. Для рассматриваемой области (

,
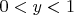
) функция

убывает с ростом

, поэтому уравнение

имеет всего один корень, обозначим его

. Для сходимости последовательности необходимо:

(именно эту область мы сейчас и нашли), но вот достаточно ли? Я пытался доказать достаточность, исследуя

, а именно: хотел доказать, что условие

для всех

всегда (при всех

,

в рассматриваемой области) влечёт за собой

для всех

. Отсюда до достаточности рукой подать, но попытки идти этим путём приводят к громоздким выражениям, которые я ниасилил. Так что, возможно, найдены ещё не все области расходимости.



