Если я возьму производную по-честному:

Здесь у Вас неправильное обозначение производной. Должно быть

поскольку это полная производная.
К моменту процитированного сообщения Вам уже объясняли, что есть частная производная

, которая вычисляется в
предположении, что все переменные независимые (ну, так уж она определяется, и совершенно не важно, какие у них там зависимости на самом деле), и полная производная

, при вычислении которой все зависимости обязательно учитываются. Что ещё тут непонятно? Что, такие серьёзные сомнения?
Есть даже специальная формула полной производной: если задана функция
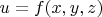
, где

и

являются функциями переменной

, то полная производная

вычисляется по формуле

Обратите внимание на разницу в обозначениях производных. Впрочем, эту формулу Вы должны знать.



