Чтобы разобраться со сложными понятиями, можно сначала их рассмотреть на самых простых примерах.
Мотивация, слишком масштабная для сделанного
(Оффтоп)
Посмотрим на примере матриц

над

-

- такие понятия:
- матрицы невырожденные, вырожденные, рангов

- группы, перечисленные на диаграмме
![$$\xymatrix{
\mathrm{SZ}(\mathbb{R}^2)\cong \{\pm 1\} \ar@{^(->}[r] \ar@{^(->}[d]
& \mathrm{Z}(\mathbb{R}^2)\cong \mathbb{R}^* \ar@{->>}[r]^{\det \cong z^2} \ar@{^(->}[d]
& (\mathbb{R}^*)^2\cong \mathbb{R}^+ \ar@{^(->}[d] \\
\mathrm{SL}(2,\mathbb{R}) \ar@{^(->}[r] \ar@{->>}[d]
& \mathrm{GL}(2,\mathbb{R}) \ar@{->>}[r]^{\det} \ar@{->>}[d]
& \mathbb{R}^* \ar@{->>}[d] \\
\mathrm{PSL}(2,\mathbb{R}) \ar@{^(->}[r]
& \mathrm{PGL}(2,\mathbb{R}) \ar@{->>}[r]
& \mathbb{R}^*/(\mathbb{R}^*)^2\cong \{\pm 1\}
}$$ $$\xymatrix{
\mathrm{SZ}(\mathbb{R}^2)\cong \{\pm 1\} \ar@{^(->}[r] \ar@{^(->}[d]
& \mathrm{Z}(\mathbb{R}^2)\cong \mathbb{R}^* \ar@{->>}[r]^{\det \cong z^2} \ar@{^(->}[d]
& (\mathbb{R}^*)^2\cong \mathbb{R}^+ \ar@{^(->}[d] \\
\mathrm{SL}(2,\mathbb{R}) \ar@{^(->}[r] \ar@{->>}[d]
& \mathrm{GL}(2,\mathbb{R}) \ar@{->>}[r]^{\det} \ar@{->>}[d]
& \mathbb{R}^* \ar@{->>}[d] \\
\mathrm{PSL}(2,\mathbb{R}) \ar@{^(->}[r]
& \mathrm{PGL}(2,\mathbb{R}) \ar@{->>}[r]
& \mathbb{R}^*/(\mathbb{R}^*)^2\cong \{\pm 1\}
}$$](https://dxdy-03.korotkov.co.uk/f/a/3/4/a342eb9f7e1aa51bc24917f1f534687b82.png)
-  - полная линейная группа - группа невырожденных матриц;
- полная линейная группа - группа невырожденных матриц;
-  - специальная линейная группа - группа матриц с
- специальная линейная группа - группа матриц с  ;
;
-  - проективная группа - группа проективных преобразований проективной прямой
- проективная группа - группа проективных преобразований проективной прямой  ;
;
-  - проективная специальная линейная группа;
- проективная специальная линейная группа;
возможно, 
Также на диаграмме:
 - изоморфизм групп;
- изоморфизм групп;  - мономорфизм = инъективный гомоморфизм групп;
- мономорфизм = инъективный гомоморфизм групп;  - эпиморфизм = сюръективный гомоморфизм групп;
- эпиморфизм = сюръективный гомоморфизм групп;
 (по прямой линии) - короткая точная последовательность, то есть наложено условие, что образ первого гомоморфизма равен ядру второго гомоморфизма; частные случаи короткой точной последовательности - прямое и полупрямое произведения;
(по прямой линии) - короткая точная последовательность, то есть наложено условие, что образ первого гомоморфизма равен ядру второго гомоморфизма; частные случаи короткой точной последовательности - прямое и полупрямое произведения;
-  - центр группы
- центр группы  - группа всех скалярных преобразований в
- группа всех скалярных преобразований в 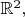 то есть матриц, пропорциональных единичной;
то есть матриц, пропорциональных единичной;
центр группы есть та её часть, которая коммутирует со всей группой;
-  - центр группы
- центр группы  - группа всех скалярных преобразований с
- группа всех скалярных преобразований с  ; она изоморфна группе всех корней 2-й степени из единицы в
; она изоморфна группе всех корней 2-й степени из единицы в  ;
;
-  - мультипликативная группа
- мультипликативная группа  (группа обратимых действительных чисел), а
(группа обратимых действительных чисел), а  - подгруппа положительных чисел;
- подгруппа положительных чисел;
-  - квадраты действительных чисел, то есть в данном случае, опять положительные числа.
- квадраты действительных чисел, то есть в данном случае, опять положительные числа.
также интерес представляют
-

и

- ортогональные группы - группы, сохраняющие евклидово и минковское скалярное произведение;
-

и

- специальные ортогональные группы - с

;
возможно,

и алгебра(ы)

(многовато как-то для начала, это всё скорее благие пожелания, записанные, чтобы не забыть; ну и приоритеты надо будет расставить).
Дальше эти выводы можно будет попытаться расширить на размерность 3 и на поле

----------------
Матрицы

задаются четырьмя действительными числами

- и таким образом, образуют 4-мерное действительное пространство. Бо́льшие размерности и бо́льшие поля вряд ли возможно будет визуализовать.
Рассмотрим вырожденные матрицы -

Заодно, это множество матриц

причём

- единственная точка

Множество

- это 3-мерная гиперповерхность, коразмерности 1.
Изображение множеств в 4-мерном пространстве непросто. Попробуем зафиксировать 4-ю координату

и взять несколько сечений. Они будут

- седловидными поверхностями, либо при

- двумя плоскостями

Из этого списка поверхностей пока не совсем ясно устройство 3-поверхности. Заметим, что

- однородное уравнение, и потому 3-поверхность представляет собой конус с вершиной в нуле координат. Чтобы обрисовать "основание" конуса, возьмём предыдущие сечения при

и отметим на них "края" - линии пересечения этих поверхностей с 3-сферой

Это будут сферы

То есть, сферы разных радиусов для разных поверхностей. Конкретное значение

безразлично, поскольку, вспоминаем,

- однородное уравнение. И пройдёмся по разным уровням
![$d\in[-R,R].$ $d\in[-R,R].$](https://dxdy-03.korotkov.co.uk/f/e/2/2/e2288e418ccee44644534518bac3121f82.png)
И потом, из этих "краёв" надо собрать нечто целое на 3-сфере. 3-сфера сама по себе четырёхмерна. Её придётся как-то отобразить в нашем пространстве. Например, в шаре (в "стеклянном шаре"). Радиальная координата внутри шара соответствует угловой координате "от полюса

" на 3-сфере (то есть, "широте, считая от полюса"). А обычные сферические угловые координаты внутри шара - соответствуют "координатам долготы" на 3-сфере. (
https://en.wikipedia.org/wiki/N-sphere#Spherical_coordinates) И в целом, "стеклянный шар" собирается из 2-сфер возрастающего радиуса, но внешняя сфера должна быть стянута в точку. Так что, приведённую последовательность линий надо "собирать изнутри наружу", масштабируя (каждая линия уже находится на 2-сфере в 3-мерном пространстве). Покажу процесс по стадиям, обратите внимание на середину процесса, соответствующую "переходу экватора

":
Здесь подразумевается, что на конечной стадии всё опять сошлось в точку - "в полюс

". Так что, край получившейся фигуры надо понимать как склеенную точку. Надеюсь, видно, что получился тор. Вот он, красавчик, немного с другого ракурса:
Полная же поверхность

представляет собой конус над этим тором. Надеюсь, теперь это можно себе представить. (Каждая пара противоположных точек на этом торе соответствует прямой, проходящей через начало координат.)
Полная линейная группа - группа невырожденных матриц

делится на две несвязные компоненты: над тором и под тором.
(черновики)
где единичная матрица?
повернём оси координат в e=a+d, f=a-d, g=b+c, h=d-c. Поверхность

приводится к главным осям:

сигнатура
