P vs NP .

[Ioda]

mihaild в сообщении #1385858 писал(а):

Нет, это следует из того, что можно явно предъявить МТ, распознающую этот язык за полиномиальное время.

Так в чем ,тогда проблема предложенного мной множества ?

Ioda в сообщении #1385803 писал(а):

перенумеруем $P$ (беря пары МТ и язык) и потребуем от всех языков ,которые возьмём в наше множество ,непустоты и пустого пересечения со всеми остальными языками рассматриваемого множества ,и именно с этим множеством (мною построенным) будем работать.

[mihaild]

Я что-то при первом чтении пропустил "перенумерум $P$" - зачем?
Пока что я понял, что вы хотите взять последовательность пар $(M_i, L_i)$, где $L_i \in P$, $M_i$ (видимо) распознает $L_i$ и работает полиномиальное время, $L_i \neq \varnothing$, $\forall i, j: i \neq j \rightarrow L_i \cap L_j = \varnothing$. Так?

Если да, то я предлагаю взять некоторую конкретную последовательность, чтобы было проще следить. А именно: перенумеруем все слова, скажем что $L_i = \{x_i\}$, $M_i$ будет на словах длины $n$ работать $2^{|x_i|} \cdot n$.

[Ioda]

mihaild в сообщении #1385972 писал(а):

Если да, то я предлагаю взять некоторую конкретную последовательность, чтобы было проще следить. А именно: перенумеруем все слова, скажем что $L_i = \{x_i\}$, $M_i$ будет на словах длины $n$ работать $2^{|x_i|} \cdot n$.

Я что-то снова не понял.

mihaild в сообщении #1385972 писал(а):

скажем что $L_i = \{x_i\}$, $M_i$ будет на словах длины $n$ работать $2^{|x_i|} \cdot n$.

Если это условие верно ,то по-моему нельзя говорить о принадлежности определенных вами языков классу $P$ .

[mihaild]

Ioda в сообщении #1385973 писал(а):

Если это условие верно ,то по-моему нельзя говорить о принадлежности определенных вами языков классу $P$ .

А по-моему можно. По-моему машина, работающая на слове длины $n$ время $c \cdot n$, где $c$ - некоторая константа, работает полиномиальное время.
Взял язык, взял машину, распознающую его за полиномиальное время, что вам не нравится? Никаких ограничений, связывающих эти МТ друг с другом, задано не было.

[Ioda]

mihaild в сообщении #1385974 писал(а):

где $c$ - некоторая константа,

Проблема в том ,что $c$ ,определенная по-вашему, не константа ,и вообще зависит от длины слова. Где я ошибся?

[mihaild]

Ioda в сообщении #1385977 писал(а):

Где я ошибся?

В порядке кванторов.
Для каждого слова $y$ мы рассматриваем МТ $M(y)$, которая, получив на вход слово $x$, за время $2^{|y|} \cdot |x|$ выдает $1$, если $x = y$, и $0$ если $x = y$. Упражнения:
-для каждого слова $y$ укажите явно язык, распознаваемый МТ $M(y)$
-для каждого слова $y$ докажите, что МТ $M(y)$ работает полиномиальное время; найдите явно степень этого полинома

[Ioda]

mihaild в сообщении #1385978 писал(а):

-для каждого слова $y$ укажите явно язык, распознаваемый МТ $M(y)$

Думаю ,что $L(M(y))=\{y\}$ . Так?

mihaild в сообщении #1385978 писал(а):

-для каждого слова $y$ докажите, что МТ $M(y)$ работает полиномиальное время; найдите явно степень этого полинома

То ,что полиномиально долго ,думаю из-за принадлежности каждого языка классу $P$ .

mihaild в сообщении #1385978 писал(а):

выдает $1$, если $x = y$, и $0$ если $x = y$.

Наверное ,второе равенство должно было быть знаком неравенства. Пусть $x\ne y$ ,тогда за время не превышающее линейное мы получим $0$ . Если $x=y$ ,то за время $2^{|y|}\cdot |y|$ ,которое уже не полиномиально, мы получим $1$ . Так?

[mihaild]

Ioda в сообщении #1385983 писал(а):

Думаю ,что $L(M(y))=\{y\}$ . Так?

Да.

Ioda в сообщении #1385983 писал(а):

То ,что полиномиально долго ,думаю из-за принадлежности каждого языка классу $P$ .

Нет конечно. То, что машина распознает некоторый язык из $P$, еще не означает, что она сама работает полиномиальное время. Один и тот же язык могут распознавать разные машины, работающие разное время.

Ioda в сообщении #1385983 писал(а):

Работаю в вашем множестве , вследствие некоструктивности моего.

Неконструктивность - не приговор, вполне допустимо рассматривать множества без явного их построения. Но довольно часто бывает полезно посмотреть на какие-то "странные" подходящие под условия примеры.

Ioda в сообщении #1385983 писал(а):

Наверное ,второе равенство должно было быть знаком неравенства

Да, опечатка.

Ioda в сообщении #1385983 писал(а):

Пусть $x\ne y$ ,тогда за время не превышающее линейное мы получим $0$ . Если $x=y$ ,то за время $2^{|y|}\cdot |y|$ мы получим $1$ ,это уже не полином. Так?

Так, понятно, зря я начал говорить словами о времени работы.
Сформулируйте определение понятия "время работы МТ $M$ полиномиально". Потом подставьте в это определение МТ $M(y)$ и покажите, что она ему удовлетворяет.

[Ioda]

mihaild в сообщении #1385984 писал(а):

Сформулируйте определение понятия "время работы МТ $M$ полиномиально". Потом подставьте в это определение МТ $M(y)$ и покажите, что она ему удовлетворяет.

Извините , ступил. По сути , $2^{|y|}\cdot |y|$ это константа .

-- 04.04.2019, 19:45 --

mihaild в сообщении #1385984 писал(а):

Но довольно часто бывает полезно посмотреть на какие-то "странные" подходящие под условия примеры.

Давайте рассмотрим на вашем примере принцип моего доказательства ,быть может ,тогда найдем ошибку.

[mihaild]

Т.е. зачем-то взяли такое множество языков (каждый язык ровно из одного слова). Что дальше?

[Ioda]

mihaild в сообщении #1386004 писал(а):

Что дальше?

Построить аналогичное (по тем же правилам) множество для $NP$ .
Дальше ,если вы читали доказательство ,то просто подставить в неравенство ,которое выводим и получить оценки временной сложности для образа взятого слова (тут возможны вопросы). Если не читали , то прочитать хотя бы часть доказательства . Если хотите ,конечно.

[mihaild]

Ioda в сообщении #1386286 писал(а):

Построить аналогичное (по тем же правилам) множество для $NP$ .

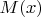
Нет, так не пойдет. Во-первых, напишите, и зафиксируйте, какое именно множество мы взяли - пар вида $\langle\{x\}, M(x)\rangle$, где $x$ - слово, а $M(x)$ - МТ, распознающая язык $\{x\}$ и на словах длины $n$ работающая $2^{|x|} n$? Подтвердите явно, или напишете другой вариант.
Во-вторых, причем тут вообще $P$, и что за множество вам нужно для $NP$? Почему не подойдет то же? (любая детерменированная МТ является и недетерменированной)

Ioda в сообщении #1386286 писал(а):

Если хотите ,конечно

Нет, не хочу, и вряд ли кто-то захочет. Пока что ушло две страницы на то, чтобы только подойти к определению то ли функции $t(x)$, то ли $T(x)$ (я не очень понимаю, какой и что от них нужно). Никаких следов отношения эквивалентности уже не осталось, как и ваших $X_P$ и $X_{NP}$. Поэтому нужно написать явно.

На всякий случай напомню

Forum Administration в сообщении #27358 писал(а):

3.2. Публикуя свои взгляды на форуме, автор принимает на себя обязательства вежливо, четко и по существу отвечать на вопросы, заданные участниками обсуждения вежливо, четко и по существу. Безусловно обязательны ответы на вопросы, заданные несколькими участниками, представителями администрации или участниками форума, имеющими статус "Заслуженный". В случае невыполнения этих обязательств, игнорирования вопросов, а также если ответы и аргументы автора признаются участниками форума неубедительными или бессодержательными, тема может быть закрыта.
3.3. Не допускаются аргументы типа: "Я уже отвечал на этот вопрос, а если вы мой ответ не поняли - это не мое дело". Ответить на вопрос так, чтобы его поняли и приняли, является заботой автора темы. Не допускаются отписки вида: "Перечитайте внимательно мой текст, там есть ответ на ваш вопрос". Если вопрос задан, то это значит, что участник не видит ответа на него. Автор темы обязан либо ответить на вопрос, либо процитировать свой ответ, если полагает, что он уже был дан раньше.

Проблема в том, что вы изъясняетесь так, что понять вас совершенно невозможно. Чтобы получилось что-то осмысленное ваши тексты нужно переделывать настолько сильно, что получается очень много вариантов переделки, причем в результате всё равно получаются совершенно очевидно неверные утверждения.
Я искренне верю что любой человек может научиться понимать математические тексты и выражать свои мысли так, чтобы их можно было понять, и я готов попробовать помочь вам научиться, но для этого вам нужно прилагать усилия и не считать мои замечания "придирками". Я понимаю, что у вас есть ощущение, что в голове у вас стройная картина. У меня тоже часто бывает такое ощущение. Но как раз сложности с формальным выражением этой картины как раз являются очень хорошим признаком того, что картины на самом деле нет, только ощущение.

[Ioda]

mihaild в сообщении #1386297 писал(а):

Во-первых, напишите, и зафиксируйте, какое именно множество мы взяли - пар вида $\langle\{x\}, M(x)\rangle$, где $x$ - слово, а $M(x)$ - МТ, распознающая язык $\{x\}$ и на словах длины $n$ работающая $2^{|x|} n$?

Возникает следующая ситуация:

mihaild в сообщении #1385972 писал(а):

Я что-то при первом чтении пропустил "перенумерум $P$" - зачем?

Мое множество (его построение) предполагает также ,что $\operatorname{pr_1} : X \to P$ ,где $X$ - рассматриваемое множество пар ,а $\operatorname{pr_1}$ - проектор по первому аргументу ,и он является биекцией для данных множеств. Если я не оговорил этого ранее ,это действительно мой прокол, но оговариваю это сейчас. У меня есть подозрения ,что ваше множество не подходит.

mihaild в сообщении #1386297 писал(а):

Почему не подойдет то же? (любая детерменированная МТ является и недетерменированной)

Ну ,в доказательстве ,я неявно иду от противного . То есть, предполагая неравенство классов ,показываю ,что из этого следует их равенство.

mihaild в сообщении #1386297 писал(а):

но для этого вам нужно прилагать усилия и не считать мои замечания "придирками"

Я готов приложить усилия ,и прошу простить за именование ваших замечаний "придирками" ,тут я тоже,к сожалению, допустил вольность речи

[mihaild]

Ioda в сообщении #1386304 писал(а):

$\operatorname{pr_1} : X \to P$ ,где $X$ - рассматриваемое множество пар ,а $\operatorname{pr_1}$ - проектор по первому аргументу ,и он является биекцией для данных множеств

Т.е. на самом деле вы хотите рассмотреть такое множество пар вида (язык, МТ), что каждый язык из $P$ является первым элементом ровно одной пары? (т.е. по сути это множество является функцией из $P$ в МТ, которое каждому языку сопоставляет некоторую МТ)
Это совсем другое требование. И да, под него мое множество не подходит, в нем далеко не все языки из $P$.

Но вроде бы раньше вы хотели чтобы языки, являющиеся первыми элементами этих пар, не пересекались. Уже не хотите?

[Ioda]

mihaild в сообщении #1386307 писал(а):

Но вроде бы раньше вы хотели чтобы языки, являющиеся первыми элементами этих пар, не пересекались. Уже не хотите?

Если я не могу соблюсти оба условия , то выберу это ,с оговоркой ,что время распознавания некоторого слова $x$ в возможном пересечении языков $L_1$ и $L_2$ будет равно $\min\limits_{}(t(M_1,x),t(M_2,x))$ . Надеюсь мы уже определили ,что значат выражения $t(M,x)$ .