Рассмотрим цилиндрический конденсатор. Внутренний проводник пусть имеет потенциал 1 В, внешний - 0 В, радиус внешнего проводника - 1. Потенциал

, где

--- радиус внутреннего проводника. Будем стремить

к нулю:
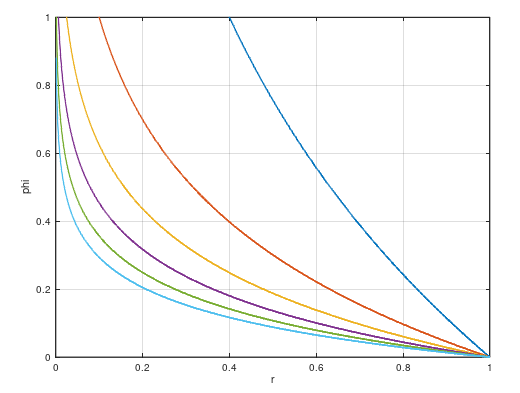
При стремлении радиуса внутреннего проводника к нулю:
1) максимальная напряжённость поля будет стремиться к бесконечности;
2) в каждой точке напряжённость поля будет стремиться к нулю;
3) в каждой точке, за исключением точек, расположенных на оси, потенциал будет стремиться к нулю;
4) заряд и ёмкость будут стремиться к нулю.
В пределе напряжённость поля везде равна нулю, потенциал везде, за исключением точек на оси, равен нулю, заряд и ёмкость равны нулю.
Наверное что-то подобное будет происходить и в рассматриваемом случае. Т.е. при стремлении радиуса проволочки к нулю потенциал будет стремиться к потенциалу, который был без проволочки (везде, за исключением точек кривой, определяющей проволочку), а максимальная напряжённость - к бесконечности. Только вот как это доказать?



