Ну, по той же формуле получается

, хотя перебором выходит
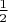
.
Перебором как раз таки

выходит, но не по вашей формуле.
-- Пн янв 14, 2019 12:52:03 --Эта формула будет верной, если домножить на количество способов расставить 2 бубновых, 3 пиковых и 5 червовых тузов по 10 местам. Это количество не будет меняться в ваших вариантах, поэтому можно не находить, а обозначить

. Но лучше найти, попрактикуетесь, хотя бы.
-- Пн янв 14, 2019 12:56:02 --Далее - как может меняться состав колоды? Вижу 12 вариантов:
1) б 25, п 25, ч 50
2) б 25, п 30, ч 45
3) б 30, п 25, ч 45
4) б 15, п 35, ч 50
5) б 20, п 35, ч 45
6) б 15, п 40, ч 45
7) б 15, п 30, ч 55
8) б 20, п 25, ч 55
9) б 15, п 25, ч 60
10) б 10, п 35, ч 55
11) б 25, п 20, ч 55
12) б 25, п 35, ч 40
Почему только пятерками меняете? б 20, п 31, ч 49 ничем не хуже, а во многом даже и лучше, чем приведенные варианты.
И да, знаменатель в вариантах тоже везде одинаков, поэтому тоже можете его вынести и не учитывать при сравнении. Останется хорошо просматриваемая функция от трех переменных с одним условным равенством плюс границы.



