Я еще вижу, по вашему поведению на форуме, что вы быстро теряете интерес, не доводите задачи до конца до наступления полной ясности для вас самого, так чтобы вы могли объяснить в вашем решении каждый шаг, каждую букву. Лично мне это не кажется правильной привычкой, но навязывать это мнение не буду - вот один раз пишу, и всё.
Должен сказать, что насчет данной привычки вы были бы правы только до 31 декабря того года - в новой году, с 1 января мне что-то в голову ударило - я вдруг изменился и стал решать задачи по другому. Скорее всего вы сейчас усмехнулись, но это факт - не знаю почему, но я вдруг стал получать огромное удовольствие от аккуратного решения задач: все должно быть понятно и аккуратно расписано, почерк должен быть красивым, все вычисления должны быть проведены аккуратно, все выкладки расписаны, чтобы вероятность ошибиться была минимальной. Раньше из-за того, что я считал эту процедуру скучной и неинтересной, я на всех олимпиадах делал тупейшие ошибки, поскольку не привык делать все аккуратно. Я раньше думал, что задача человека - решать исключительно сложные и содержательные задачи, а совершать даже самые простейшие выкладки - задача исключительно для компа. Сейчас я полностью осознал, что крош цена "математику/физику",который думает, ведь чтобы решать сложные задачи нужно аккуратно решать простые подзадачи, иначе никогда к решению сложной задачи прийти будет нельзя! Моя жизнь это показала. Сейчас я вообще получаю эстетическое удовольствие от аккуратно записанных решений - у меня черновики стали выглядеть лучше, чем раньше выглядели чистовики, а вероятность ошибок почти снизилась до нуля! Аккуратность, как показал опыт, играет ключевую роль. Я понял, что процедура аккуратной записи решения вовсе не скучна, а очень интересна - она также приятна, как создание фигурок оригами, в которые ты душу вкладываешь. Я недавно также заметил, что как только я, например от усталости, перестаю все подробно и скрупулезно расписывать, то сразу же нарываюсь на ошибки, так что мне еще предстоит поработать над выносливостью. Похоже мне придется быть аккуратным даже если я перестаю получать от этого удовольствие из-за усталости. Ну или пойти отдохнуть.
Что касается до этой задачи, то я расписал ее как попало, поскольку я вообще не знал, как решать задачу - а так получается, что попытки решения задачи есть, и на карантин тему не отправят. А за задержку доведения данной задачи до конца(что происходит после моего головного "удара" 31 декабря) могу ответить - я чрезвычайно сильно загружен, я составил список из 8 олимпиад, которые дают льготу БВИ в МФТИ, накачал кучу вариантов по каждой олимпиаде по физике и математике и начал все прорешивать. До начала большинства заключительных этапов осталось примерно 40 дней, столько же вариантов я скачал, так что по норме я должен решать 1 вариант в день. Поскольку каждый вариант рассчитан на 4 часа + возможно придется потратить дополнительное время на разбор неверно решенных задач/на поиск ошибок в моем решении, то "обработка" варианта в среднем занимает много времени, так что график у меня забит. Сегодня я еле нашел время, чтобы разобраться с задачей, которую я выставил на форуме. На форум я теперь буду заходить намного реже и стараться больше разбираться с задачами самому - слишком много времени на форум уходит. Хорошо хоть, что перечневые олимпиады, к которым я себя натаскиваю, не состоят из настолько сложных олимпиадных задач, что без помощи я не обойдут - мой уровень вполне достаточен для их решения, просто нужно очень хорошо отработать аккуратность и скрупулезность, а так бы уходило еще куча времени на обсуждение огромного числа олимпиадных задач из перечня, а времени у меня уже и так нет почти. Эх, как же жаль, что благодатный "удар" по голове, резко повышающий мою аккуратность, трудоспособность и мотивацию, не мог произойти раньше - "ударило" бы меня в классе 8 или хотя бы в 9, я был наверное сейчас бы ехал на межнар по физике и/или математике!
Думая над данной задачей, я только сейчас осознал, что оказывается подход решения большого класса физических задач, опирающихся на исчисление бесконечно малых, абсолютно одинаков и заключается в следующем:
Вот у нас есть некая система, она разбивается на

подсистем и для них записываются

уравнений, содержащих неизвестные величины

, причем сумма
![$\[\sum\limits_{i = 1}^n {{x_i}} \]$ $\[\sum\limits_{i = 1}^n {{x_i}} \]$](https://dxdy-03.korotkov.co.uk/f/6/2/e/62e36bd078e28f6bfdc808a0a3e7a4fe82.png)
равна искомой величине

. При этом, каждое из

уравнений содержит некие поправки
![$\[{\sigma _i}\]$ $\[{\sigma _i}\]$](https://dxdy-02.korotkov.co.uk/f/5/a/1/5a169d02c9ac78fbb4d4c772f0ceac0282.png)
, которые нам неизвестны. Таким образом, искомая величина

оказывается равной
![$$\[x = \sum\limits_{i = 1}^n {{x_i}} = \sum\limits_{i = 1}^n {{A_i} + \sum\limits_{i = 1}^n {{\sigma _i}} } \]$$ $$\[x = \sum\limits_{i = 1}^n {{x_i}} = \sum\limits_{i = 1}^n {{A_i} + \sum\limits_{i = 1}^n {{\sigma _i}} } \]$$](https://dxdy-04.korotkov.co.uk/f/3/b/e/3bef249d81712d76dbf6c90ff72a678882.png)
где

- известные величины, содержащиеся в

уравнениях. Здесь, казалось бы, требуется еще

для определения всех поправок
![$\[{\sigma _i}\]$ $\[{\sigma _i}\]$](https://dxdy-02.korotkov.co.uk/f/5/a/1/5a169d02c9ac78fbb4d4c772f0ceac0282.png)
, однако в высшей математике идут на следующую хитрость. Считая, что уравнение
![$\[x = \sum\limits_{i = 1}^n {{x_i}} \]$ $\[x = \sum\limits_{i = 1}^n {{x_i}} \]$](https://dxdy-01.korotkov.co.uk/f/8/e/3/8e3f159d37869ce545070ff36bc05cd482.png)
верно для всех натуральных

, рассматривают предел
![$$\[x = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{x_i}} \]$$ $$\[x = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{x_i}} \]$$](https://dxdy-02.korotkov.co.uk/f/1/c/1/1c16c3b8ac74a38bfcbd766915f4530582.png)
Видимо, надо еще доказать, что такой "трюк" можно совершить,что уравнение остается верным и в пределе, но я пока не владею строгим формализмом математического анализа (не читал Зорича), поэтому вынужден опускать это доказательство.
Тогда для

имеет место равенство:
![$\[x = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{A_i} + \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{\sigma _i}} } \]$ $\[x = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{A_i} + \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{\sigma _i}} } \]$](https://dxdy-01.korotkov.co.uk/f/0/c/9/0c97860c53312dd56ae468cc11e0fed682.png)
Далее обычно доказывают,

Я также не знаю, как это сделать строго, поэтому такие доказательства я всегда опускал.
Итак,как оказывается, суть в том, что если устремить

к бесконечности, то неизвестные поправки зануляются.
На этом ,насколько я понял, основаны еще 2 подхода высшей математики:
1) Рассматривают некую подсистему сложной системы, в частности, рассматривают участок функции от

до
![$\[x + \Delta x\]$ $\[x + \Delta x\]$](https://dxdy-03.korotkov.co.uk/f/a/1/7/a17445f1c460f4e89346141d616a13cf82.png)
, записывают уравнение с неизвестной поправкой
![$\[\sigma \]$ $\[\sigma \]$](https://dxdy-03.korotkov.co.uk/f/e/7/d/e7da7b4ff3f45d306d319462a4ff25a482.png)
.
2) Добавляют некую подсистему к сложной системе, в частности, в нашей задаче с пружиной прикрепляют кусок пружины сверху/снизу, записывают уравнение с неизвестной поправкой
![$\[\sigma \]$ $\[\sigma \]$](https://dxdy-03.korotkov.co.uk/f/e/7/d/e7da7b4ff3f45d306d319462a4ff25a482.png)
на искомое удлинение пружины.
Далее рассматривают предел данной системы, если можно так выразиться, при котором влияние подсистемы на всю систему стремиться к нулю - устремляют
![$\[\Delta x\]$ $\[\Delta x\]$](https://dxdy-02.korotkov.co.uk/f/9/4/d/94d31dc1a3991505cb1b687db83ffb5982.png)
к нулю, уменьшают до нуля массу добавляемого куска пружины. При этом оказывается, что записанное уравнение с поправкой в пределе сохраняет силу(что надо как то доказать), а сама поправка стремиться к нулю(что тоже надо доказать). И тогда получается, что в пределе уравнение содержит только известные величины и задача решена.
Другой вопрос, правда, встанет, если окажется, что поправка в пределе не стремится к нулю и тогда ошибка становится все больше и больше, она может быть конечной или вообще бесконечной, тогда я не знаю, что делать.
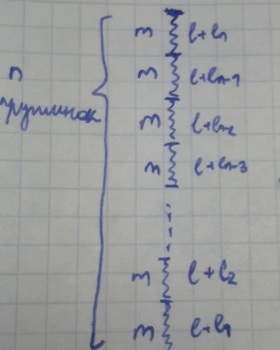
Решим задачу с пружиной. Разобьем пружину массой

на

одинаковых пружинок с жесткостями

и начальными длинами

(без деформации). Эта величина связана с жесткостью
![$\[{k_\Sigma }\]$ $\[{k_\Sigma }\]$](https://dxdy-02.korotkov.co.uk/f/1/0/d/10d296b7d2d710a70074a42639cf9b9482.png)
всей пружины так:
![$\[\frac{1}{k} = \frac{1}{{n{k_\Sigma }}}\]$ $\[\frac{1}{k} = \frac{1}{{n{k_\Sigma }}}\]$](https://dxdy-04.korotkov.co.uk/f/f/a/a/faa1d7379f9deb240aa073cb10a9734c82.png)
. Далее запишем

уравнений для каждой пружины
![$$\[\begin{gathered}
k{l_1} = 0g + {F_1} \hfill \\
k{l_2} = mg + {F_2} \hfill \\
\vdots \hfill \\
k{l_n} = (n - 1)mg + {F_n} \hfill \\
\end{gathered} \]$$ $$\[\begin{gathered}
k{l_1} = 0g + {F_1} \hfill \\
k{l_2} = mg + {F_2} \hfill \\
\vdots \hfill \\
k{l_n} = (n - 1)mg + {F_n} \hfill \\
\end{gathered} \]$$](https://dxdy-01.korotkov.co.uk/f/0/c/d/0cd9e12a8a377943b219c240da666e6d82.png)
Здесь

- те самые поправки, связанные с тем, что на удлинение каждой пружины сказывается не только масса нижеприкреплённых пружинок, но и масса этой же пружины.
Из данных уравнений найдем
![$\[\Delta l\]$ $\[\Delta l\]$](https://dxdy-02.korotkov.co.uk/f/1/e/1/1e1c40d1ee3c467d068db6569e837f7c82.png)
:
![$$\[\Delta l = \sum\limits_{i = 1}^n {{l_i} = } \frac{{mg}}{k}\sum\limits_{i = 1}^n {(i - 1)} + \frac{1}{k}\sum\limits_{i = 1}^n {{F_i}} = \frac{{mg}}{k}\frac{{n(n - 1)}}{2} + \frac{1}{k}\sum\limits_{i = 1}^n {{F_i}} = \frac{{Mg}}{{2{k_\Sigma }}}\frac{{n - 1}}{n} + \frac{1}{k}\sum\limits_{i = 1}^n {{F_i}} \]$$ $$\[\Delta l = \sum\limits_{i = 1}^n {{l_i} = } \frac{{mg}}{k}\sum\limits_{i = 1}^n {(i - 1)} + \frac{1}{k}\sum\limits_{i = 1}^n {{F_i}} = \frac{{mg}}{k}\frac{{n(n - 1)}}{2} + \frac{1}{k}\sum\limits_{i = 1}^n {{F_i}} = \frac{{Mg}}{{2{k_\Sigma }}}\frac{{n - 1}}{n} + \frac{1}{k}\sum\limits_{i = 1}^n {{F_i}} \]$$](https://dxdy-01.korotkov.co.uk/f/0/7/3/0739d719b6ccbc31ba4c728121f3edd582.png)
Далее как то доказывается, что это выражение сохраняется и при
![$\[{n \to \infty }\]$ $\[{n \to \infty }\]$](https://dxdy-02.korotkov.co.uk/f/9/0/b/90b75d2a8be42c1005a5ae6d8f75062482.png)
, и записывается:
![$$\[\Delta l = \frac{{Mg}}{{2{k_\Sigma }}}\mathop {\lim }\limits_{n \to \infty } \frac{{n - 1}}{n} + \frac{1}{k}\mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{F_i}} = \frac{{Mg}}{{2{k_\Sigma }}} + \frac{1}{k}\mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{F_i}} \]$$ $$\[\Delta l = \frac{{Mg}}{{2{k_\Sigma }}}\mathop {\lim }\limits_{n \to \infty } \frac{{n - 1}}{n} + \frac{1}{k}\mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{F_i}} = \frac{{Mg}}{{2{k_\Sigma }}} + \frac{1}{k}\mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{F_i}} \]$$](https://dxdy-04.korotkov.co.uk/f/7/3/a/73aaa4f311ae37a8b788e9f4db8b7a8082.png)
Далее надо как-то показать, что
![$$\[\mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{F_i}} = 0\]$$ $$\[\mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {{F_i}} = 0\]$$](https://dxdy-02.korotkov.co.uk/f/d/5/d/d5d19c4546e16c4fcb9a765365ca907a82.png)
Если доказать, что уравнение сохраняет силу при
![$\[{n \to \infty }\]$ $\[{n \to \infty }\]$](https://dxdy-02.korotkov.co.uk/f/9/0/b/90b75d2a8be42c1005a5ae6d8f75062482.png)
, и что при
![$\[{n \to \infty }\]$ $\[{n \to \infty }\]$](https://dxdy-02.korotkov.co.uk/f/9/0/b/90b75d2a8be42c1005a5ae6d8f75062482.png)
поправка стремиться к

, то задача будет решена.
-- 12.01.2019, 19:27 --Вообще говоря, поскольку я пока не вдумывался в определение предела, то мне неочевидно, почему если разность между приближенным значением и точным в пределе стремиться к

, то можно добиться того, что приближенное значение станет точным. Ну да, мы можем сделать так, чтобы разница между точным и приближенным значением была сколь угодно близка к

, но почему из этого следует, что точное и приближенное выражение будут равны, ведь никто не говорил, что разница будет равна В ТОЧНОСТИ

?
-- 12.01.2019, 19:29 --Из этой же оперы равенство
![$\[1 = 0,(9)\]$ $\[1 = 0,(9)\]$](https://dxdy-01.korotkov.co.uk/f/0/9/c/09c69d4b9b48dbabdc04a8c95e4c2b1482.png)
которое я никогда не принимал на 100%. Ну да, правая часть все ближе и ближе к

, но кто сказал, что она и итоге станет равной

в пределе? Не переваривает мой мозг пока такие вещи. Не могу я принять этой факт только из интуитивных соображений.