Здравствуйте, всем,
Задача следующая: есть последовательность данных, более или менее хорошо укладывающаяся на экспоненту вида

. Надо получить параметры

,

и

. Характерный вид кривой приведен на скриншоте.
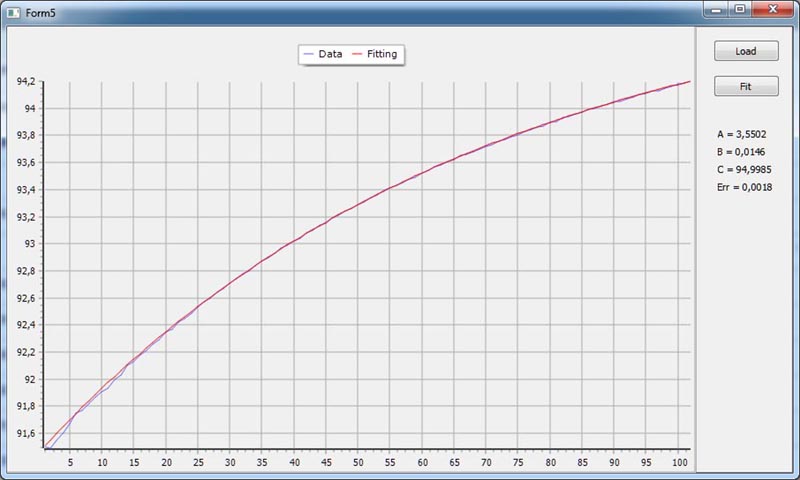
.
Для нахождения параметров берем, например, каждую 20-ю точку и по пяти таким выбранным точкам минимизируем сумму разностей квадратов

. Вопрос в том, как задать область поиска минимума, так, чтобы он там точно был? Я только очень приблизительно знаю характер ожидаемой кривой.
Пока что придумал только так:
Код:
// здесь yv[i] - массив исходных данных
// A
krx[0][0] := 0;
krx[0][1] := 4 * (yv[length(yv) - 1] - yv[0]);
// B
krx[1][0] := 0;
krx[1][1] := 0.1;
// C
krx[2][0] := yv[length(yv) - 1];
krx[2][1] := krx[2][0] + 4 * (yv[length(yv) - 1] - yv[0]);
// точка старта поиска минимума
x[0] := 0.5 * (krx[0][1] + krx[0][0]);
x[1] := 0.5 * (krx[1][1] + krx[1][0]);
x[2] := 0.5 * (krx[2][1] + krx[2][0]);
//
Можно, конечно, задать какие-то очень широкие пределы, но я не уверен, что при этом не возникнет проблем с самим алгоритмом минимизации. Поэтому и возник вопрос, а нельзя ли как-то очень грубо оценить параметры, хотя бы

и

, поскольку от

зависимость, очевидно, квадратичная. Кроме того, я, в принципе, знаю его верхний предел, поскольку это конкретная физическая величина.
Заранее спасибо за любые подсказки.



