Да, кстати, у вас опечатка в условии - так система имеет бесконечно много решений
Какая система?
У вас первое и третье уравнения в сумме откровенно намекают на ответ.

Это уравнение намекает на отсутствие целых корней в кольце вычетов по модулю три?
Знаете ли Вы, что кольцо вычетов по модулю простого числа является полем, и почему ?
Да, потому что кольцо ассоциативное, коммутативное, с ненулевой единицей, в котором всякий ненулевой элемент имеет обратный
Рассмотрим поле вычетов по модулю

. Найдите

,

,

, , где

,

Я не знаю что значат вот такие обозначения:
Цитата:

,

Если это обыкновенные числа три и пять, то:



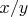
и

не знаю, нет решений?