Не ограничивая общности можно считать

симметричная матрица (

). Если она к тому же вещественна (и тогда эрмитова), то необходимо наложить условие отрицательной определенности

(т.е.


).
Однако

может быть и комплексной матрицей с отрицательно определенной вещественной частью. Тогда с помощью линейной замены это сводится к случаю

. Т.е.

, где

вещественная и симметричная. Но тогда с помощью ортогональной замены мы сохраняем

и приводим

к диагональному виду. Т.е. все опять сводится к одномерному случаю, но теперь комплексному. А его можно сделать обычно: рассмотрев

введя полярные координаты.
Да, я полагал, что

. Но

с любым комплексным вектором

сводится сдвигом к

. Если сдвиг комплексный, то интегрирование получается по
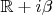
и ТФКП доказывает, что это то же, что и с

.
Условие "

" может быть заменено на "

и

невырождена" и даже на некоторую комбинацию: "

и

невырождена" (вроде бы)



