Добавлю комплементарное:
Paul IvanovВ формуле для
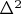
опечатались вы или кто-то из подготавливавщих учебник.
Смысл простой, но чтобы его увидеть, используем альтернативное обозначение

. Применим теперь к

несколько разных

(сначала первую, потом вторую и т. д.) — это и будет

-я конечная разность

с шагами

, та, которая вас интересует.
В приложениях нередко все

друг с другом совпадают, тогда их не упоминают явно и иногда даже считают равными 1 — в частности, для функций целочисленного аргумента такие более всего похожи на производную для функций вещественного аргумента.
∗ ∗ ∗ ∗ ∗
Кстати Зорич тут может напугать излишней общностью, но при этом почему-то останавливается на полдороги, определив только опережающие конечные разности, но не запаздывающие.



