Если

а ток единичный синфазный меандр, то

и как тут останется только первая гармоника?
Формула

не является ни разложением мгновенной мощности в ряд Фурье, ни следствием разложения мгновенной мощности в ряд Фурье.
Ладно, я думаю мы ходим вокруг терминов для синусов и потому для несинусов получается бессмысленная фигня.
Круг замкнулся только сейчас. Ибо не фигня получается. Ниже некоторые тезисные утверждения. Если у Вас остались с ними несогласия, предлагаю обсудить в ЛС.
1. Понятия полной и активной мощности естественным образом расширяются на несуносидальные периодические сигналы. Используются те же формулы, что и для синусоидальных.
2. Физический смысл активной мощности остаётся тем же самым - средняя переданная от источника в нагрузку мощность.
3. Физический смысл полной мощности, как произведения действующего напряжения на действующий ток - остается тем же самым. Слово "полная" смысл теряет (см. ниже).
4. Можно формально ввести понятие реактивной мощности.
5. Однако, вместо равенства

имеем неравенство

. Поэтому название "полная мощность" теряет смысл. Более правильно говорить "кажущаяся мощность".
6. Более того, как показано на примере выше, может оказаться так, что
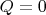
, а

.
7. Поэтому для нелинейных нагрузок удобнее использовать отношение

, которое называют power factor, PF
8. Если напряжение остается синусоидальным, а ток - нет, то PF красиво выражается через произведение, где
а) один множитель выражается через коэффициент гармоник (по току)
б) другой множитель отражает "реактивную" составляющую главной компоненты.



