Физическое понимание дифференциала

[SomePupil]

Дифференциал $-$ это малая величина. А строгое определение, границы применимости... это все там. Дифференциал есть, например, элемент площади $dS$, элемент объема $dV,$ малый угол $d\varphi...$ А линейное отображение, определенное на приращениях аргумента, "хорошо приближающее" исходную функцию $-$ это все... Там.

[wrest]

SomePupil в сообщении #1338825 писал(а):

Дифференциал $-$ это малая величина.

Малая по сравнению с чем?

[SNet]

Спасибо всем! Многое стало проясняться, а для большего понимания почитаю сегодня учебник по матанализу на эти темы и, если будут вопросы, напишу их сюда.

P.S. Тогда это ещё один минус в пользу книги Зельдовича-Яглома: она культивирует в читателе понимание производной именно в смысле Лейбница.

[rustot]

Возвращаясь к самому первому сообщению, по-моему так и осталось без ответа (или я не заметил?) следующее:

SNet в сообщении #1338519 писал(а):

И в итоге выясняется, что вектору скорости ортогонален $\frac{d\vec\tau}{dt}$, но не $d\vec\tau$. Почему?

Откуда взялось это "но не"? Дифференциал единичного вектора именно что ортогонален этому единичному вектору.
Если обозначит единичный вектор как $\hat{k}$, то $\hat{k}\cdot d\hat{k} \equiv 0$

$d(\vec{n}) = d(n\hat{n}) = \hat{n}\cdot dn + n\cdot d\hat{n}$ тут второе слагаемое именно ортогонально к $\hat{n}$ а значит и к $\vec{n}$

[SNet]

rustot

upgrade в сообщении #1338344 писал(а):

Так получается, что в любой момент времени $\vec{\tau} \perp d\vec{\tau}$

arseniiv в сообщении #1338349 писал(а):

Только потому что $\lVert\vec\tau\rVert = 1$. Плюс, не $d\vec\tau$, а $\vec\tau'$.

Если я неправильно понял это сообщение, то прошу прощения у arseniiv за наговаривание.

[Munin]

SNet в сообщении #1338842 писал(а):

Тогда это ещё один минус в пользу книги Зельдовича-Яглома: она культивирует в читателе понимание производной именно в смысле Лейбница.

Эту книгу не стоит воспринимать как учебник. Она даёт предварительное знакомство с предметом, как раз в ситуации, когда по физике пользоваться математическим аппаратом уже нужно, а на математике его ещё не дали. После этого, конечно, должно следовать полноценное изучение курса матанализа по стандартным изложениям.

[Pphantom]

Все же не очень понятно, откуда взято противопоставление учебников физики и учебников математики.

Дифференциал (первого порядка функции одной переменной, поскольку ничего другого в первом семестре и не требуется, то слова про формы можно честно оставить на потом) - это линейная часть приращения функции (не обязательно "малая" или даже "бесконечно малая"). Такое определение корректно с точки зрения математики и вполне пригодно с точки зрения физики.

В упомянутом учебнике Матвеева, кстати, в этом смысле все сделано довольно аккуратно: в нем записывается производная как отношение дифференциалов (но не появляется отдельное определение дифференциала), в дальнейшем в виде дифференциалов записываются элементарные перемещения и т.п., но нигде не говорится, что если величина обозначена таким образом, то она является малой. В общем, если не пытаться додумывать самостоятельно то, что в учебнике отсутствует, то получается ничему не противоречащая "заглушка", достаточная до появления честного изложения в курсе матанализа.

Кстати, в других сколько-нибудь популярных учебниках (для определенности - русскоязычных) ситуация аналогична. У Сивухина есть явное обсуждение того, почему вариант с "бесконечно малыми" некорректен и какой смысл вкладывали ранее и вкладывают сейчас в подобную запись. Савельев в целом похож на Матвеева. В Берклеевском курсе понятие дифференциала тщательно избегается, обозначения Лейбница используются только как вариант обозначения производной (и соответствующим образом вводятся).

[SomePupil]

wrest в сообщении #1338833 писал(а):

Малая по сравнению с чем?

Оценка порядка малости $-$ это все Там. А те, кто матану не нюхал, когда пишут в школе, например $d\vec B = I \frac{\vec r \times d\vec r}{r^3},$ они пишут это и наслаждаются жизнью. Наслаждаются жизнью и крепче спят, между прочим.

[upgrade]

rustot в сообщении #1338846 писал(а):

Откуда взялось это "но не"?

Если у меня, то из неверного понимания приращения $\vec{\tau}$ - это не приращение длины, а приращение направления - небольшой поворот, насколько я понимаю $\vec{\tau}'$ - тоже вектор, который показывает направление малого поворота единичного вектора.

[Munin]

Pphantom в сообщении #1338854 писал(а):

Дифференциал (первого порядка функции одной переменной, поскольку ничего другого в первом семестре и не требуется

Простите, а как же дифференцирование векторов?

[Pphantom]

Munin в сообщении #1338870 писал(а):

Простите, а как же дифференцирование векторов?

Векторная функция одной переменной в принципе тоже подходит. А если серьезно, то этот случай ничем не отличается (опять-таки если не додумывать самостоятельно что-то лишнее, вроде упомянутого выше отнесения "приращения вектора" не к вектору, а почему-то к его длине).

[Munin]

Pphantom в сообщении #1338911 писал(а):

А если серьезно, то этот случай ничем не отличается

Мы-то это понимаем. Но педагогически надо, видимо, как-то это рассмотреть отдельно и пояснить. Соседняя тема («Единичный вектор в кинематике.») вся целиком посвящена непониманию этого случая.

[Guvertod]

SNet, постараюсь объяснить развернуто, как мне кажется, лучше всего вам это сейчас воспринимать:

Какое определения дифференциала?

Дифференциал функции $f(x)$ в точке $x$ есть функция $df(h)=f'(x)h$, где $h$ - любое число.

Для красоты и удобства можно ввести $dx=h$ - "дифференциал аргумента в точке $x$" и записать:

$$f'(x)=\frac{df}{dx}$$

И далее уже не важно, чему именно равно это $dx=h$, дифференциалы используются тут как связанные переменные ( называя их переменными, я подразумеваю их значение, формально они функции) и никогда явно не приравниваются к конкретным числам!

Часто, особенно в физике, нет разделения на функцию $f(x)$ и аргумент $x$, а есть просто различные величины ,зависящие друг от друга.
(в данном случае я расписываю все для одномерного случая, когда величина явно выражается через одну другую*).
И в этом смысле совершенно не важно, что изначально было принятно за $h$, а что за "дифференциал функции".

Поэтому можно так же (если такая функция $x(f)$ есть) положить и $dx=x'(f) h$, $h=df$, так или иначе мы придем к конкретной линейной связи между переменными $dx$ и $df$.
Можно записывать связь с третьей (при параметризации) :

$$df=f'_{t}dt$$

$$dx=x'_{t}dt$$

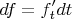
Зачем это нужно?

В первую очередь введение дифференциалов позволяет нам комфортнее работать с производными. Например, мы можем сокращать их (значения - это же просто числа!):

$$\frac{df}{dy}\frac{dy}{dx}=\frac{df}{dx}$$

Ничего нового мы тут не получили (формула для производной композиции известна, а условия эквивалентны условиям на возможность введения такого определения), но согласитесь, это выглядит нагляднее и приятнее.

Также мы можем теперь вести записи выражений с производными в виде $Bdu=Adv$ (поделить на нужный дифференциал и получить соответствующую производную всегда успеем!).
И так далее.

Но если дифференциалы принимают значения в виде обычных чисел, то почему их часто неформально называют "бесконечно малыми"?

1)Во-первых, с точки зрения физики, если мы говорим о величине вроде скорости $x'_{t}=v$, то, подразумевая, что измерить время и расстояние можно не сколько угодно малыми (нас ограничивает шкала линейки и часов), можем записать

$$v \approx \frac{\Delta x}{\Delta t}$$

( $\Delta x$ и $\Delta t$ - маленькие, насколько возможно, значения изменений расстояния и времени).
Чем более мелкое изменение этих величин мы можем измерить, тем формула точнее. В этом смысле можно неформально трактовать запись $v=\frac{dx}{dt}$ как случай "предельно точного измерения".
То есть когда $\Delta x=dx$ и $\Delta t=dt$ "бесконечно малые".
В физике порой их можно условно считать очень малыми, но конечными значениями (в зависимости от задачи).

2) Часто допускается "слишком вольное" обращение с дифференциалом:
Например, если нужно найти производную от $y=x^2$ , то мы должны формально взять предел $h \to 0$ выражения

$$\frac{(x+h)^2-x^2}{h}$$

(хотя бы интуитивно вы эту операцию уже понимаете).
И тут "возникает соблазн" после подставления определения $h=dx$ приравнять числитель сразу к $dy$: $$dy=(x+dx)^2-x^2, что неверно (ведь $dy=f'(x)dx$)!

Однако, если мы положим $dx^2=0$, то равенство станет верным (интуитивно должно быть понятно, почему в таких случаях так получается)!

Поэтому, удобно при всех таких вычислениях записывать и нелинейную связь между дифференциалами, "пренебрегая" (просто убирая их) величинами "другого порядка" (чтобы получить правильную линейную связь).
В этом смысле можно сказать так же, что $dx$ - "бесконечно малая величина" и выражения типа

$$dx+dx^2=dy$$

есть на самом деле

$$dx=dy$$

(т.к "прибавление бесконечно малой к числу ничего не изменит", $1+dx=1$)

Поэтому имеет место быть и такое понимание-определение, но повторюсь, что оно неформальное.

Что насчет интегрирования?

Смысл значка $dx$ в записи $\int dx f(x)$ вовсе не соответствует введенному определению,
он именно неразделимый с значком интеграла значок !
Но все же, например, при замене переменных, оказывается, что он ведет себя точно также:

$$\int dyf(y)=\int dxy'f(y(x))$$

И вообще, с этим обозначением нам становится психологически более комфортнее переходить от дифференциальной записи $y'_{x}=g(x)$ к

$$y=\int dx g(x)$$

(обоснование которого совсем не связано с понятием дифференциала)
Мы как-бы можем теперь воспринимать это как формальное навешивание $\int$ на выражение

$$dy=g(x)dx$$

Поэтому целесообразно условно обобщить определение:

функция $df $ $\to$ значок $df$

И просто подразумевать, что мы можем свободно выполнять с дифференциалом все подобные манипуляции (раз математически это же корректно!) и это есть суть одно и тоже.

* В многомерном случае все также обобщается, дифференциал $f$ в $x_{a}$ есть $df=\sum\limits_{}^{}\frac{\partial f (x_a)}{\partial x_{i}}dx_{i}$.
С ним работаем в этом же духе, не забывая различать отношение дифференциалов и частные производные.
Аналогично с многомерным интегрированием по $\int dx_1..dx_n$, там дифференциалы при замене переменных ведут себя "как положено"...

Так же уже должно быть понятно, что такое дифференциал вектора $d\vec{r}$ (можно определить хотя бы по компонентам), что используется в физике.

Часто бывает удобно ставить дифференциал перед большим выражением типа $d(g(x)+f(x))$ (понятно что это есть), поэтому окончательно обобщаем:

дифференциал $\to$ значок дифференцирования $d$

Этого общего неформального понимания для работы с выражениями в физике должно быть вам достаточно.

[upgrade]

Guvertod в сообщении #1338976 писал(а):

Смысл значка $dx$ в записи $\int dx f(x)$ вовсе не соответствует введенному определению,
он именно неразделимый с значком интеграла значок !

то есть так
$\int (y) \cdot (dx)=\int (dx) \cdot (y)$
делать нельзя?

[Guvertod]

upgrade
Не в этом смысле. Но эта формула никакой информации не несет, где писать - слева или справа - вопрос соглашений.
(лично я просто теперь привык слева, потому что мне направо детерминант метрики варьировать...)