Есть доказанная теорема о том, что

, при

. При это в википедии есть утверждение, что доказано, что существует бесконечно много простых чисел отличающихся на 246. Оно было доказано неким Пэйсом Нильсеном в 2014 году. Я видимо не очень понимаю первое утверждение, раз считаю, что оно противоречит второму. Как я рассуждал, производная функции
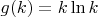
- возрастающая функция. Это значит, что

. Так как
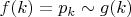
, то найдется такое

, что для всех

. А это значит, что количество таких пар конечно. Где у меня ошибка в рассуждениях?