Вот как получается так, что математика подправляет все косяки, как, например, неугаданное направление тока?
Дело в том, что вы на самом деле не выбираете направление тока. Вы выбираете направление
положительного тока. То есть просто фиксируете
способ кодирования направления.
Давайте рассмотрим, например, первый закон Кирхгофа: сумма втекающих в узел токов равна сумме истекающих. Это формулировка для "незакодированных" токов (то есть положительных). Найдём как должна звучать формулировка для "закодированных" токов, то есть токов со знаком, где знак кодирует направление.
Сначала выберем фиксированный способ кодирования: все истекающие токи будем считать положительными, а все втекающие — отрицательными. Нетрудно сообразить, что тогда правило для "закодированных" токов будет такое: сумма всех токов равна нулю.
Теперь пусть для тока в одной или нескольких из ветвей правило кодирования обратное: втекающий ток считается отрицательным, а истекающий — положительным. Как изменится формулировка закона Кирхгофа? Понятно, что надо поменять у соответствующих слагаемых знак = перенести слагаемое в другую часть, то есть формулировка превращается в такую: сумме токов в ветках, у которых положительным направлением считается направление "к узлу", равна сумме токов, у которых положительным направлением считается направление "от узла".
Теперь давате рассмотрим две совершенно разные ситуации. В первой из них у нас имеется узел, в который токи

и

втекают, а токи

и

вытекают. Отметим на рисунке направления токов (именно токов, а не каких-то "положительных направлений"):
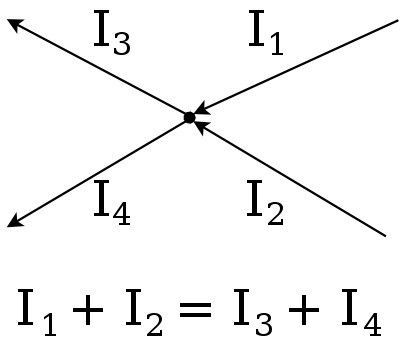
Запишем закон Кирхгофа по нашему
первому правилу, получим:

Теперь посмотрим на ту же картинку иначе. Пусть на ней отмечены не направления токов, а положительные направления. Запишем закон Кирхгофа по нашему
последнему правилу, получим

Теперь заметим, что
формы записанных законов совпадают (при этом содержание у них
разное: в первом случае в законе стоят (положительные) величины токов, текущих в известных направлениях, а в втором — величины со знаками, где знаки кодируют
неизвестные направления токов). Можно считать это удачным совпадением. И вот,
используя это совпадение, мы можем переформулировать наше последнее правило следующим образом.
1) Выберем направления токов произвольным образом.
2) Запишем правило Кирхгофа, считая, что токи текут в выбранных нами направлениях.
3) Если в результате окажется, что некоторый ток имеет отрицательное значение, это значит, что выбранное направление было неверным.