Ради закрепления материала решил перечитать "Введение в алгебру" Кострикина. Я заметил, что в этом учебнике есть факты, которые при первом прочтении кажутся не особо важными, но на самом деле в дальнейшем используются при доказательстве некоторых теорем.
В связи с этим появился вопрос. В параграфе "Отношения эквивалентности. Факторизация отображений" показывается, как можно разложить произвольное отображение
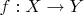
в произведение сюръективного отображения

и инъективного

. Здесь

-- следующее отношение эквивалентности:

.
Зачем нам может потребоваться разлагать отображение в произведение сюръективного и инъективного отображения? Чтобы увидеть некоторое сходство с теоремой о гомоморфизме для групп? Или для того, чтобы определять сюръективность

по сюръективности

?
Второй вопрос касается линейной оболочки. Множество

всех линейных комбинаций векторов

называют их линейной оболочкой.
Далее в некоторых местах говорится:
Цитата:

-- линейная оболочка в

Цитата:
для каждой линейной оболочки

, входящей в множество
Чем в приведенных выше цитатах линейная оболочка отличается от подпространства?



